题目内容
已知函数
 ,给出下列命题:①
,给出下列命题:① 必是偶函数;②当
必是偶函数;②当 时,
时, 的图象关于直线
的图象关于直线 对称;③若
对称;③若 ,则
,则 在区间
在区间 上是增函数;④
上是增函数;④ 有最大值
有最大值 . 其中正确的命题序号是( )
. 其中正确的命题序号是( )
(A)③ (B)②③ (C)②④ (D)①②③
【答案】
A
【解析】解:当a≠0时,f(x)不具有奇偶性,①错误;
令a=0,b=-2,则f(x)=|x2-2|,
此时f(0)=f(2)=2,
但f(x)=|x2-2|的对称轴为y轴而不关于x=1对称,②错误;
又∵f(x)=|x2-2ax+b|=|(x-a)2+b-a2|,图象的对称轴为x=a.
根据题意a2-b≤0,即f(x)的最小值b-a2≥0,
f(x)=(x-a)2+(b-a2),显然f(x)在[a,+∞]上是增函数,
故③正确;
又f(x)无最大值,故④不正确.
答案:③.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目

 ,给出下列命题:
,给出下列命题: 必是偶函数;
必是偶函数; 时,
时, 对称;
对称; ,则
,则 上是增函数;
上是增函数; .
.  ,给出下列四个命题:
,给出下列四个命题: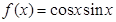 ,给出下列四个说法:
,给出下列四个说法: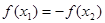 ,则
,则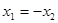 ,②点
,②点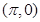 是
是 的一个对称中心,
的一个对称中心,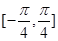 上是增函数,④
上是增函数,④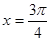 对称.
对称.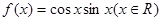 ,给出下列四个命题:
,给出下列四个命题: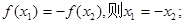 ②
②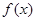 的最小正周期是
的最小正周期是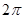 ;
;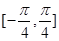 上是增函数;
④
上是增函数;
④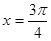 对称;
对称;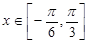 时,
时,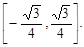 其中正确的命题为 ( )
其中正确的命题为 ( ) ,给出下列命题:①
,给出下列命题:①  的图象可以看作是由y=sin2x的图象向左平移
的图象可以看作是由y=sin2x的图象向左平移 个单位而得;②
个单位而得;② 而得;③函数y=|
而得;③函数y=| ;④
函数y=|
;④
函数y=|