题目内容
已知函数 ,给出下列四个命题:
,给出下列四个命题:①函数f(x)是周期函数;
②函数f(x)既有最大值又有最小值;
③函数f(x)的图象有对称轴;
④对于任意x∈(-1,0),函数f(x)的导函数f′(x)<0.
其中真命题的序号是 .(请写出所有真命题的序号)
【答案】分析:观察函数的解析式,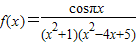 ,它是一个非奇非偶函数,由于分子的值从-1到1周期性变化,分母的值随着x的值远离原点,逐渐趋向于正无穷大,函数图象逐渐靠近x轴,由这些性质对四个命题进行判断选出正确选项
,它是一个非奇非偶函数,由于分子的值从-1到1周期性变化,分母的值随着x的值远离原点,逐渐趋向于正无穷大,函数图象逐渐靠近x轴,由这些性质对四个命题进行判断选出正确选项
解答:解:由已知函数的解析式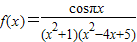
①函数f(x)是周期函数不正确,因为分母随着自变量的远离原点,趋向于正穷大,所以函数图象无限靠近于X轴,故不是周期函数;
②函数f(x)既有最大值又有最小值,由①的判断知,函数存在最大值与最小值,此命题正确;
③函数f(x)的定义域是R,且其图象有对称轴,由函数解析式可以得出,其图象周期性穿过X轴,由于分母不断增大,图象往两边延伸都无限靠近于X轴,其对称轴是x=1,此命题正确;
④由对于任意x∈(-1,0),f′(x)<0(f′(x)是函数f(x)的导函数),此命题不正确,
由于自变量从-1变化到0分母变小,而分子由-1增大到1,所以函数值的变化是由小增大,故导数恒大于等于0.此命题不正确
综上,②③正确
故答案为:②③
点评:考查了函数思想,转化思想,属中档题,是个基础题.还考查函数图象的对称变化和一元二次方程根的问题,以及函数奇偶性的判定方法等基础知识,考查学生灵活应用知识分析解决问题的能力,数形结合法是解答本类题的重要方法.本题函数解析式复杂,不利于判断
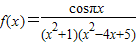 ,它是一个非奇非偶函数,由于分子的值从-1到1周期性变化,分母的值随着x的值远离原点,逐渐趋向于正无穷大,函数图象逐渐靠近x轴,由这些性质对四个命题进行判断选出正确选项
,它是一个非奇非偶函数,由于分子的值从-1到1周期性变化,分母的值随着x的值远离原点,逐渐趋向于正无穷大,函数图象逐渐靠近x轴,由这些性质对四个命题进行判断选出正确选项解答:解:由已知函数的解析式
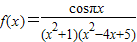
①函数f(x)是周期函数不正确,因为分母随着自变量的远离原点,趋向于正穷大,所以函数图象无限靠近于X轴,故不是周期函数;
②函数f(x)既有最大值又有最小值,由①的判断知,函数存在最大值与最小值,此命题正确;
③函数f(x)的定义域是R,且其图象有对称轴,由函数解析式可以得出,其图象周期性穿过X轴,由于分母不断增大,图象往两边延伸都无限靠近于X轴,其对称轴是x=1,此命题正确;
④由对于任意x∈(-1,0),f′(x)<0(f′(x)是函数f(x)的导函数),此命题不正确,
由于自变量从-1变化到0分母变小,而分子由-1增大到1,所以函数值的变化是由小增大,故导数恒大于等于0.此命题不正确
综上,②③正确
故答案为:②③
点评:考查了函数思想,转化思想,属中档题,是个基础题.还考查函数图象的对称变化和一元二次方程根的问题,以及函数奇偶性的判定方法等基础知识,考查学生灵活应用知识分析解决问题的能力,数形结合法是解答本类题的重要方法.本题函数解析式复杂,不利于判断

练习册系列答案
相关题目




 ,给出下列四个命题:
,给出下列四个命题: ②
② 的最小正周期是
的最小正周期是 ;
; 上是增函数; ④
上是增函数; ④ 对称;
对称; 时,
时, 其中正确的命题为
其中正确的命题为  ,给出下列四个说法:
,给出下列四个说法: ,则
,则 ;
; 的最小正周期是
的最小正周期是 ;
; 上是增函数;
上是增函数; 对称.
对称. ,给出下列四个命题:①函数的图象关于点(1,1)对称;②函数的图象关于直线
,给出下列四个命题:①函数的图象关于点(1,1)对称;②函数的图象关于直线 对称;③函数在定义域内单调递减;④将函数图象向左平移一个单位,再向下平移一个单位后与函数
对称;③函数在定义域内单调递减;④将函数图象向左平移一个单位,再向下平移一个单位后与函数 的图象重合。其中正确命题的序号是__________
的图象重合。其中正确命题的序号是__________