Question

设F是椭圆

x2

4

+y2=1的右焦点，椭圆上的点与点F的最大距离是M，最小距离是m，则椭圆上与点F的距离等于

1

2

(M+m)的点的坐标是

（0，±1）

．

Answer 1

分析：根据椭圆上的点与点F的最大距离，最小距离分别是：M=a+c，n=a-c，从而得出

1

2

（M+m）=a，故椭圆上与点F的距离等

1

2

（M+m）的点是短轴的两个顶点即可解决问题．

解答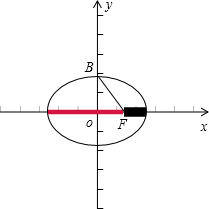：解：∵椭圆上的点与点F的最大距离为M，最小距离是m，
∴M=a+c，n=a-c
∴

1

2

（M+m）=a，
则椭圆上与点F的距离等a的点是短轴的两个顶点，
其坐标为：（0，±1）．
故答案为：（0，±1）．

点评：本小题主要考查椭圆的简单性质等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．