题目内容
 如图,数表满足:
如图,数表满足:(1)第n行首尾两数均为n;
(2)表中递推关系类似杨辉三角,记第n(n>1)行第2个数为f(n).根据表中上下两行数据关系,可以求得当n≥2时,f(n)=
分析:依据“中间的数从第三行起,每一个数等于它两肩上的数之和”则第二个数等于上一行第一个数与第二个数的和,即有an+1=an+n(n≥2),再由累加法求解.
解答:解:(1)依题意an+1=an+n(n≥2),a2=2
所以a3-a2=2a4-a3=3,an-an-1=n
累加得 an-a2=2+3+…+(n-1)=
所以 an=
-
+1(n>2)
当n=2时 a2=
×22-
×2+1=2,也满足上述等式
故 an=
-
+1
所以a3-a2=2a4-a3=3,an-an-1=n
累加得 an-a2=2+3+…+(n-1)=
| (n+1)(n-2) |
| 2 |
所以 an=
| n2 |
| 2 |
| n |
| 2 |
当n=2时 a2=
| 1 |
| 2 |
| 1 |
| 2 |
故 an=
| n2 |
| 2 |
| n |
| 2 |
点评:本题通过三角数表构造了一系列数列,考查了数列的通项及求和的方法,还考查了数列间的关系,入题较难,知识点,方法活,属中档题

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 如图数表满足:(1)第n(n>1)行首尾两数均为n,第一行为一个数1;(2)表中的递推关系:从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和.现记第n(n>1)行第2个数为an,如a2=2,a3=4,a4=7,a5=11…,则可以得到递推关系:an=
如图数表满足:(1)第n(n>1)行首尾两数均为n,第一行为一个数1;(2)表中的递推关系:从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和.现记第n(n>1)行第2个数为an,如a2=2,a3=4,a4=7,a5=11…,则可以得到递推关系:an=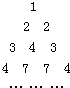 如图,数表满足:
如图,数表满足:
