题目内容
设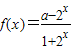
，其中实常数a＞-1．（Ⅰ）若函数f（x）是奇函数，求a的值； （Ⅱ）求函数f（x）的值域．
【答案】分析：（Ⅰ）若奇函数在x=0处有定义，则f（0）等于0，代入函数解析式即可
（Ⅱ）从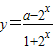
中反解出2x，利用2x＞0，解得函数f（x）的值域．
解答：解：（Ⅰ）∵函数f（x）是奇函数，∴f（0）=0⇒a=1
（Ⅱ）由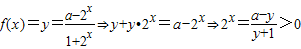
，得：-1＜x＜a
所以函数f（x）的值域为[-1，a]
点评：本题考查了函数的奇偶性，和函数值域的求法，特别是奇函数的性质，解题时要善于转化，提高解题速度
（Ⅱ）从
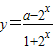中反解出2x，利用2x＞0，解得函数f（x）的值域．解答：解：（Ⅰ）∵函数f（x）是奇函数，∴f（0）=0⇒a=1
（Ⅱ）由
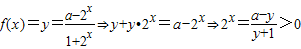，得：-1＜x＜a所以函数f（x）的值域为[-1，a]
点评：本题考查了函数的奇偶性，和函数值域的求法，特别是奇函数的性质，解题时要善于转化，提高解题速度
练习册系列答案
相关题目
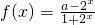，其中实常数a≥-1．
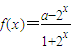，其中实常数a≥-1．
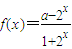，其中实常数a≥-1．