题目内容

如图，三棱柱A1B1C1―ABC的三视图中，主视图和左视图是全等的矩形，俯视图是等腰直角三角形，已知点M是A1B1的中点.

   （1）求证：面AC1M⊥AA1B1B；

   （2）求证：B1C∥平面AC1M.

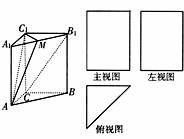
解：由三视图可知

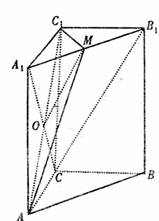
三棱柱A1B1C1―ABC为直三棱柱，底面是等腰直角三角形，

       且∠ACB=90°.

   （1）∵A1C1=B1C1，M为A1B1中点，

       ∴C1M⊥A1B1，

       又∵面A1B1C1⊥面A1B1BA，

       面A1B1C1∩面A1B1BA=A1B1，

       ∴C1M⊥面A1B1BA，

       又∵C1M面AC1M，

       ∴面AC1M⊥面A1B1BA.

   （2）连结A1C，设A1C∩AC1=0，连结MO，

       ∵A1O=CO，A1M=B1M，

       ∴MO∥B1C，

       又∵MO面AC1M，B1C面AC1M，

       ∴B1C∥面AC1M.

练习册系列答案
相关题目
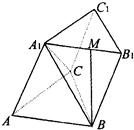精英家教网如图，三棱柱ABC-A1B1C1的底面是边长为a的正三角形，侧面ABB1A1是菱形且垂直于底面，∠A1AB=60°，M是A1B1的中点．
（1）求证：BM⊥AC；
（2）求二面角B-B1C1-A1的正切值．
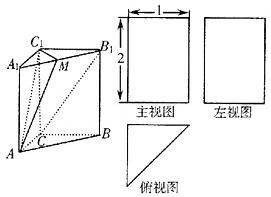精英家教网如图，三棱柱A1B1C1-ABC的三视图中，主视图和左视图是全等的矩形，俯视图是等腰直角三角形，已知点M式A1B1的中点．
（I）求证B1C∥平面AC1M；
（Ⅱ）设AC与平面AC1M的夹角为θ，求sinθ．
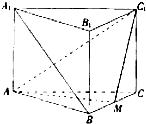如图，三棱柱ABC-A1B1C1中，侧棱与底面垂直，AB=BC=2AA1，∠ABC=90°，M是BC中点．
（Ⅰ）求证：A1B∥平面AMC1；
（Ⅱ）求直线CC1与平面AMC1所成角的正弦值；
（Ⅲ）试问：在棱A1B1上是否存在点N，使AN与MC1成角60°？若存在，确定点N的位置；若不存在，请说明理由．
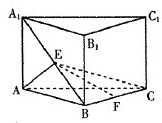如图，三棱柱ABC-A1B1 C1中，侧棱AA1⊥平面ABC，AB=BC=AA1=2，AC=2
2
，E，F分别是A1B，BC的中点．
（Ⅰ）证明：EF∥平面AAlClC；
（Ⅱ）证明：AE⊥平面BEC．
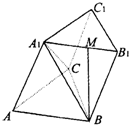如图，三棱柱ABC-A1B1C1的底面是边长为a的正三角形，侧面ABB1A1是菱形且垂直于底面，∠A1AB=60°，M是A1B1的中点．
（1）求证：BM⊥AC；
（2）求二面角B-B1C1-A1的正切值；
（3）求三棱锥M-A1CB的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网