题目内容
设集合D={平面向量},定义在D上的映射f,满足对任意x∈D,均有f(x)=λx(λ∈R且λ≠0).若|a|=|b|且a、b不共线,则〔f(a)-f(b)〕•(a+b)=______;若A(1,2),B(3,6),C(4,8),且f
)=
,则λ=______.
| (BC |
| AB |
∵均有f(x)=λx(λ∈R且λ≠0).
∴〔f(a)-f(b)〕•(a+b)=
(λ
-λ
(
+
=
λ(
2-
2)
∵|a|=|b|且a、b不共线,
∴〔f(a)-f(b)〕•(a+b)=0,
∵f(
=
,
A(1,2),B(3,6),C(4,8),
∴
=2
∴f(
=λ
=
,
λ=2
故答案为:0;2.
∴〔f(a)-f(b)〕•(a+b)=
(λ
| a |
| b)• |
| a |
| b) |
λ(
| a |
| b |
∵|a|=|b|且a、b不共线,
∴〔f(a)-f(b)〕•(a+b)=0,
∵f(
| BC) |
| AB |
A(1,2),B(3,6),C(4,8),
∴
| AB |
| BC |
∴f(
| BC) |
| BC |
| AB |
λ=2
故答案为:0;2.

练习册系列答案
相关题目
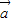 |=|
|=|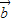 |且
|且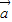 、
、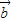 不共线,则(f(
不共线,则(f(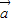 )-f(
)-f(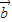 ))•(
))•(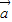 +
+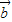 )=______;若A(1,2),B(3,6),C(4,8),且f(
)=______;若A(1,2),B(3,6),C(4,8),且f(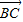 )=
)=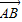 ,则λ=______.
,则λ=______.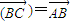 ,则λ= .
,则λ= .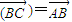 ,则λ= .
,则λ= .