题目内容
（12分）函数
＝
（1）若集合
中元素只有一个，求出此时
的值。
（2）当
时，用单调性定义证明函数
上单调递增.
＝（1）若集合
中元素只有一个，求出此时的值。（2）当
时，用单调性定义证明函数上单调递增.（1）1；（2）证明: 见解析
试题分析：（1）由f（x）=x，变形为二次方程，根据△=0，求参数k的值；
（2）由增函数的定义知对任意的1＜x1＜x2，f（x1）-f（x2）＜0，由此不等式得到x的关系式，求解即可得到证明．
证明: 略 。。。。。。。12分点评：解决该试题的关键是解题的关键是将题设中所给的条件进行正确转化如（1）中，转化一元二次方程有一根，（2）根据增函数的定义转化出关于参数的不等式．本题考查了转化化归的能力．
练习册系列答案
相关题目
｝，B＝｛
｝，则A∪B＝（ ）
，
，则M∩N中元素的个数是（ ）
，集合
，则
=______.
，集合
，则
（ ） 
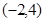
}，则M的真子集个数为（ ）
，若
，则
的值为 .
=（ ）
，
是虚数单位，集合
（整数集）和
的关系韦恩（Ｖenn）图如图所示，则阴影部分所示的集合的元素共有（ ）