题目内容
(本小题满分14分)
已知函数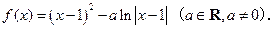
(1)当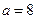 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)求函数 在区间
在区间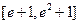 上的最小值.
上的最小值.
已知函数
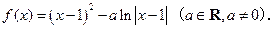
(1)当
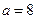 时,求函数
时,求函数 的单调区间;
的单调区间;(2)求函数
 在区间
在区间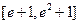 上的最小值.
上的最小值.(1)单调递减区间是
 ,
,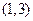
(2)当
 时,
时, 
(1)解:⑴当 时,
时,  ,
,
 .
.
由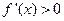 得
得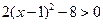 , 解得
, 解得 或
或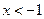 .
.
注意到 ,所以函数
,所以函数 的单调递增区间是
的单调递增区间是 .
.
由 得
得 ,解得
,解得 ,
,
注意到 ,所以函数
,所以函数 的单调递减区间是
的单调递减区间是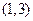 .
.
⑵当 时,
时, ,
, ,
,
由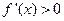 得
得 ,解得
,解得 ,
,
注意到 ,所以函数
,所以函数 的单调递增区间是
的单调递增区间是 .
.
由 得
得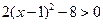 ,解得
,解得 或
或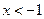 ,
,
由 ,所以函数
,所以函数 的单调递减区间是
的单调递减区间是 .
.
综上所述,函数 的单调递增区间是
的单调递增区间是 ,
, ;
;
单调递减区间是 ,
,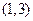 . ┅┅┅┅5分
. ┅┅┅┅5分
(2)当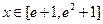 时,
时, ,
,
所以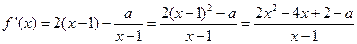 ………7分
………7分
设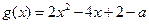 .
.
⑴当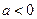 时,有
时,有 , 此时
, 此时 ,所以
,所以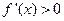 ,
, 在
在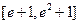 上单调递增.
上单调递增.
所以 ………… 9分
………… 9分
⑵当 时,
时, .
.
令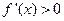 ,即
,即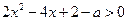 ,解得
,解得 或
或 (舍);
(舍);
令 ,即
,即 ,解得
,解得 .
.
①若 ,即
,即 时,
时,  在区间
在区间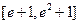 单调递减,
单调递减,
所以 .
.
②若 ,即
,即 时,
时,  在区间
在区间 上单调递减,
上单调递减,
在区间
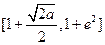 上单调递增,所以
上单调递增,所以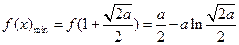 .
.
③若 ,即
,即 时,
时,  在区间
在区间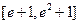 单调递增,
单调递增,
所以 . …………..13分
. …………..13分
综上所述,当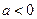 或
或 时,
时,  ;
;
当 时,
时,  ;
;
当 时,
时,  . ┅┅┅┅14分
. ┅┅┅┅14分
 时,
时,  ,
, .
.由
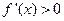 得
得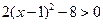 , 解得
, 解得 或
或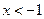 .
.注意到
 ,所以函数
,所以函数 的单调递增区间是
的单调递增区间是 .
.由
 得
得 ,解得
,解得 ,
,注意到
 ,所以函数
,所以函数 的单调递减区间是
的单调递减区间是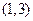 .
.⑵当
 时,
时, ,
, ,
,由
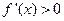 得
得 ,解得
,解得 ,
,注意到
 ,所以函数
,所以函数 的单调递增区间是
的单调递增区间是 .
.由
 得
得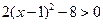 ,解得
,解得 或
或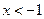 ,
,由
 ,所以函数
,所以函数 的单调递减区间是
的单调递减区间是 .
.综上所述,函数
 的单调递增区间是
的单调递增区间是 ,
, ;
;单调递减区间是
 ,
,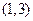 . ┅┅┅┅5分
. ┅┅┅┅5分(2)当
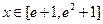 时,
时, ,
,所以
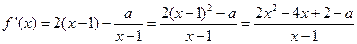 ………7分
………7分设
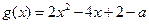 .
.⑴当
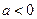 时,有
时,有 , 此时
, 此时 ,所以
,所以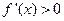 ,
, 在
在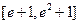 上单调递增.
上单调递增.所以
 ………… 9分
………… 9分⑵当
 时,
时, .
.令
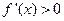 ,即
,即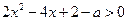 ,解得
,解得 或
或 (舍);
(舍);令
 ,即
,即 ,解得
,解得 .
.①若
 ,即
,即 时,
时,  在区间
在区间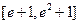 单调递减,
单调递减,所以
 .
.②若
 ,即
,即 时,
时,  在区间
在区间 上单调递减,
上单调递减,在区间

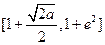 上单调递增,所以
上单调递增,所以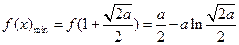 .
.③若
 ,即
,即 时,
时,  在区间
在区间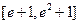 单调递增,
单调递增,所以
 . …………..13分
. …………..13分综上所述,当
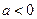 或
或 时,
时,  ;
;当
 时,
时,  ;
;当
 时,
时,  . ┅┅┅┅14分
. ┅┅┅┅14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
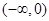 上单调递增,若f(-1)=0,则不等式f(x)<0的解集是( )
上单调递增,若f(-1)=0,则不等式f(x)<0的解集是( )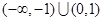
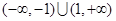
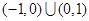
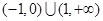
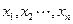 总满足
总满足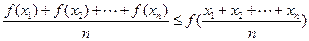 ,则称f(x)为D上的凸函数,若函数
,则称f(x)为D上的凸函数,若函数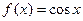 在
在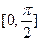 上是凸函数,则在锐角
上是凸函数,则在锐角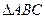 中,
中,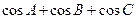 的最大值是
的最大值是 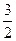
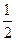


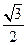
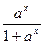 (a>0,且a≠1),〔m〕表示不超过实数m的最大整数,则
(a>0,且a≠1),〔m〕表示不超过实数m的最大整数,则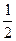 〕+〔f(-x)-
〕+〔f(-x)-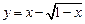 的值域为 ▲ .
的值域为 ▲ . 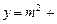
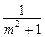 的值域为 ;
的值域为 ;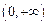 上是增函数的是( )
上是增函数的是( )