题目内容
(本小题满分12分定义在R上的函数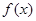 满足
满足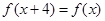 ,当
,当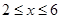 时,
时,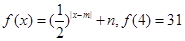 .
.
(1)求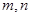 的值;
的值;
(2)比较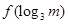 与
与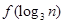 的大小.
的大小.
【答案】
解:(1)∵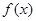 在R上满足
在R上满足 ,∴
,∴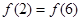 ,∴
,∴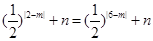
∴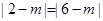 ,从而
,从而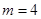 ,∴
,∴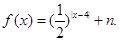 又
又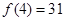 ,∴
,∴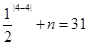 ,∴
,∴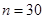
(2)由(1)可知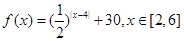
∵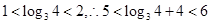 ,∴
,∴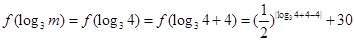
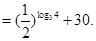
∵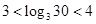 ,∴
,∴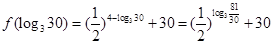
∵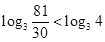 ,∴
,∴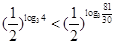 ,∴
,∴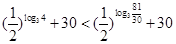
∴
【解析】略

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
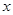 轴上,离心率为
轴上,离心率为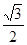 ,且经过点
,且经过点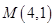 ,直线
,直线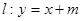 交椭圆于不同的两点A,B.(Ⅰ)求椭圆的方程;
交椭圆于不同的两点A,B.(Ⅰ)求椭圆的方程;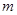 的取值范围;(Ⅲ)若直线
的取值范围;(Ⅲ)若直线 不过点M,试问
不过点M,试问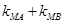 是否为定值?并说明理由。
是否为定值?并说明理由。  过抛物线
过抛物线 的焦点
的焦点 且与抛物线相交于两点
且与抛物线相交于两点 ,自
,自 向准线
向准线 作垂线,垂足分别为
作垂线,垂足分别为 .
. 的方程;
的方程; 取何实数时,
取何实数时, ,
, 都是定值;
都是定值;  (III)记
(III)记 的面积分别为
的面积分别为 ,试判断
,试判断 是否成立,并证明你的结论.
是否成立,并证明你的结论. ,
, 和定直线
和定直线 :
: ,动点
,动点 在直线
在直线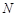 ,且
,且 .
.
 的方程并画草图;
的方程并画草图; 的直线
的直线 ,使得直线
,使得直线 ,
,  两点,且△
两点,且△ 的面积等于
的面积等于 ?如果存在,请求出直线
?如果存在,请求出直线 上一点,F1、F2是椭圆的两焦点,且满足|AF1|+|AF2|=4。
上一点,F1、F2是椭圆的两焦点,且满足|AF1|+|AF2|=4。