题目内容
两人约定在20：00到21：00之间相见（两人出发是各自独立，且在20：00到21：00各时刻相见的可能性是相等的），并且先到者必须等迟到者40分钟方可离去，则两人在约定时间内能相见的概率是（ ）
A．
| B．
| C．
| D．
|
由题意知本题是一个几何概型，设事件A为“甲乙两人能会面”，
试验包含的所有事件是Ω={（x，y）|20＜x＜21，20＜y＜21}，并且事件对应的集合表示的面积是s=1，
满足条件的事件是A={（x，y）|20＜x＜21，20＜y＜21，|x-y|＜
=
}
所以事件对应的集合表示的面积是1-2×
×
×
=
，
根据几何概型概率公式得到P=
．
则两人在约定时间内能相见的概率是
．
故选B．
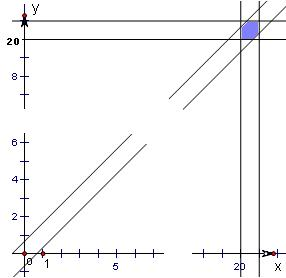
试验包含的所有事件是Ω={（x，y）|20＜x＜21，20＜y＜21}，并且事件对应的集合表示的面积是s=1，
满足条件的事件是A={（x，y）|20＜x＜21，20＜y＜21，|x-y|＜
| 40 |
| 60 |
| 2 |
| 3 |
所以事件对应的集合表示的面积是1-2×
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 9 |
根据几何概型概率公式得到P=
| 8 |
| 9 |
则两人在约定时间内能相见的概率是
| 8 |
| 9 |
故选B．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目