题目内容
已知等差数列{an}的公差不为零,且a3=5,a1,a2.a5 成等比数列
(I)求数列{an}的通项公式:
(II)若数列{bn}满足b1+2b2+4b3+…+2n-1bn=an且数列{bn}的前n项和Tn 试比较Tn与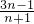 的大小.
的大小.
解:(Ⅰ)在等差数列中,设公差为d≠0,
由题意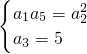 ,∴
,∴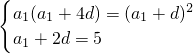 ,
,
解得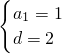 .
.
∴an=a1+(n-1)d=1+2(n-1)=2n-1.
(Ⅱ)∵b1+2b2+4b3+…+2n-1bn=an,①
b1+2b2+4b3+…+2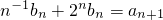 ,②
,②
②-①得2nbn+1=2,∴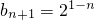 .
.
当n=1时,b1=a1=1,∴ ,
,
当n=1时,T1=a1=1,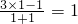 ,此时
,此时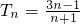 .
.
当n≥2时,Tn=1+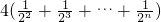
=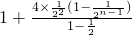 =
=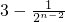 .
.
又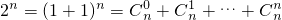 >n+1,
>n+1,
∴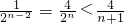 ,
,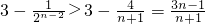 .
.
∴当n=1时,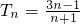 ,当n≥2时,
,当n≥2时,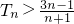 .
.
分析:(I)利用等差数列的通项公式和等比中项的定义即可得到首项和公差,即可得到通项公式;
(Ⅱ)由(I)可得:an=2n-1,由b1+2b2+4b3+…+2n-1bn=an,及b1+2b2+4b3+…+2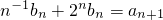 ,两式相减可得
,两式相减可得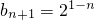 ,利用等比数列的前n项和公式即可得到Tn,与
,利用等比数列的前n项和公式即可得到Tn,与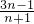 比较即可.
比较即可.
点评:熟练掌握等差数列的通项公式和等比中项的定义、等比数列的前n项和公式、二项式定理是解题的关键.
由题意
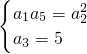 ,∴
,∴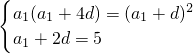 ,
,解得
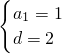 .
.∴an=a1+(n-1)d=1+2(n-1)=2n-1.
(Ⅱ)∵b1+2b2+4b3+…+2n-1bn=an,①
b1+2b2+4b3+…+2
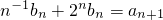 ,②
,②②-①得2nbn+1=2,∴
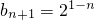 .
.当n=1时,b1=a1=1,∴
 ,
,当n=1时,T1=a1=1,
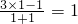 ,此时
,此时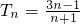 .
.当n≥2时,Tn=1+
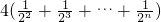
=
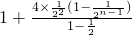 =
=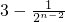 .
.又
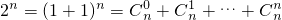 >n+1,
>n+1,∴
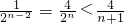 ,
,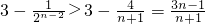 .
.∴当n=1时,
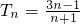 ,当n≥2时,
,当n≥2时,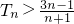 .
.分析:(I)利用等差数列的通项公式和等比中项的定义即可得到首项和公差,即可得到通项公式;
(Ⅱ)由(I)可得:an=2n-1,由b1+2b2+4b3+…+2n-1bn=an,及b1+2b2+4b3+…+2
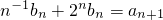 ,两式相减可得
,两式相减可得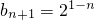 ,利用等比数列的前n项和公式即可得到Tn,与
,利用等比数列的前n项和公式即可得到Tn,与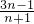 比较即可.
比较即可.点评:熟练掌握等差数列的通项公式和等比中项的定义、等比数列的前n项和公式、二项式定理是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.