题目内容
【题目】如图,已知直三棱柱ABC﹣A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1 , CC1的中点,且BE⊥B1F. 
(Ⅰ)求证:B1F⊥EC1;
(Ⅱ)求二面角C1﹣BE﹣C的余弦值.
【答案】证明:(Ⅰ)分别取BC1 , BC中点D,G,连结ED,AG, ∵ABC﹣A1B1C1是直三棱柱,且底面是正三角形,
∴AG⊥面BCC1B1 ,
又∵E,D都是中点,∴ED∥AG,则ED⊥面BCC1B1 , 可得ED⊥B1F,
已知BE⊥B1F,且BE∩ED=E,∴B1F⊥面BEC1 , 则B1F⊥EC1;
(Ⅱ)解:由(Ⅰ)知B1F⊥面BEC1 , ∴B1F⊥BC1 , 则△B1C1F∽△BB1C1 ,
∴ ![]() ,设BB1=a,则C1F=
,设BB1=a,则C1F= ![]() ,代入得a=
,代入得a= ![]() ,
,
以O为原点,OE为x轴,OC为y轴,过O作平面ABC的垂线为z轴,建立如图坐标系O﹣xyz,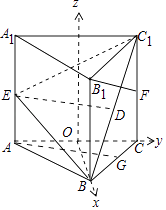
得C(0,2,0),B( ![]() ,0,0),E(0,﹣2,
,0,0),E(0,﹣2, ![]() ),
),
C1(0,2,4 ![]() ),B1(
),B1( ![]() ,0,
,0, ![]() ),F(0,2,2
),F(0,2,2 ![]() ).
).
∵B1F⊥面BEC1 , ∴平面BEC1的一个法向量为 ![]() ;
;
设平面BEC的一个法向量为 ![]() ,
,
则 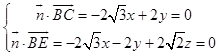 ,取x=
,取x= ![]() ,得y=3,z=
,得y=3,z= ![]() .
.
∴ ![]() .
.
∴cos< ![]() >=
>= 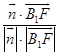 =
= ![]() =-
=- ![]() .
.
∴二面角C1﹣BE﹣C的余弦值为 ![]() .
.
【解析】(Ⅰ)分别取BC1 , BC中点D,G,连结ED,AG,推导出AG⊥面BCC1B1 , 从而ED⊥B1F,BE⊥B1F,由此能证明B1F⊥面BEC1 , 进一步得到B1F⊥EC1;(Ⅱ)以O为原点,OE为x轴,OC为y轴,过O作平面ABC的垂线为z轴,建立空间直角坐标系O﹣xyz,利用向量法能求出二面角C1﹣BE﹣C的余弦值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
