题目内容
下列命题中为真命题的是
①“若x2+y2≠0,则x,y不全为零”的否命题; ②“等腰三角形都相似”的逆命题; ③“若m>1,则不等式x2+2x+m>0的解集为R”的逆否命题.( )
①“若x2+y2≠0,则x,y不全为零”的否命题; ②“等腰三角形都相似”的逆命题; ③“若m>1,则不等式x2+2x+m>0的解集为R”的逆否命题.( )
分析:①先写出“若x2+y2≠0,则x,y不全为零”的否命题,再判断其否命题的真假;②先写出“等腰三角形都相似”的逆命题,再判断其逆命题的真假;③先判断“若m>1,则不等式x2+2x+m>0的解集为R”,的真假,再判断其逆否命题的真假.
解答:解:①“若x2+y2≠0,则x,y不全为零”的否命题是:
“若x2+y2=0,则x,y全为零”,是真命题;
②“等腰三角形都相似”的逆命题是:
“相似的三角形都是等腰三角形”,是假命题;
③“若m>1,则不等式x2+2x+m>0的解集为R”,
∵m>1,∴△=4-4m<0,
∴“若m>1,则不等式x2+2x+m>0的解集为R”是真命题,
故③“若m>1,则不等式x2+2x+m>0的解集为R”的逆否命题是真命题.
故选B.
“若x2+y2=0,则x,y全为零”,是真命题;
②“等腰三角形都相似”的逆命题是:
“相似的三角形都是等腰三角形”,是假命题;
③“若m>1,则不等式x2+2x+m>0的解集为R”,
∵m>1,∴△=4-4m<0,
∴“若m>1,则不等式x2+2x+m>0的解集为R”是真命题,
故③“若m>1,则不等式x2+2x+m>0的解集为R”的逆否命题是真命题.
故选B.
点评:本题考查命题的真假判断及其应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
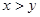 ,则
,则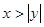 ”的逆命题
”的逆命题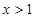 ,则
,则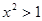 ”的否命题
”的否命题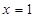 ,则
,则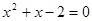 ”的否命题
”的否命题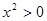 ,则
,则