题目内容
已知函数 f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求 的最大值;
的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程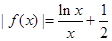 是否有实数解 .
是否有实数解 .
(1)-1
(2)
(3)方程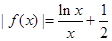 无实数解
无实数解
解析试题分析:解:(1)当 时,
时,
 ,当
,当 时,
时,
 在区间
在区间 上为增函数,
上为增函数,
当 时,
时, ,
, 在区间
在区间 上为减函数,
上为减函数,
所以当 ,
, 有最大值,
有最大值, 。 3分
。 3分
(2)∵ ,若
,若 ,则
,则 在区间(0,e]上恒成立,
在区间(0,e]上恒成立, 在区间(0,e]上为增函数,
在区间(0,e]上为增函数, ,
, ,舍去,
,舍去,
当 ,
,

 在区间(0,e]上为增函数,
在区间(0,e]上为增函数, ,∴
,∴ ,舍去,
,舍去,
若 ,当
,当 时,
时,
 在区间
在区间 上为增函数,
上为增函数,
当 时,
时,  ,
, 在区间
在区间 上为减函数,
上为减函数, ,
, ;
;
综上 。 8分
。 8分
(3)当 时,
时, 恒成立,所以
恒成立,所以 ,
,
令 ,
, ,当
,当 时,
时,
 在区间
在区间 上为增函数,
上为增函数,
当 时,
时,
 在区间
在区间 上为减函数,
上为减函数,
当 时,
时, 有最大值
有最大值 ,所以
,所以 恒成立,
恒成立,
方程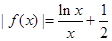 无实数解。 12分
无实数解。 12分
考点:导数的运用
点评:主要是考查了导数在研究函数单调性以及最值的运用,属于基础题。

练习册系列答案
相关题目
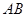 长为2m,跳水板距水面
长为2m,跳水板距水面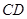 的高
的高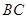 为3m,
为3m, =5m,
=5m,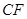 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点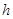 m(
m(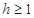 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.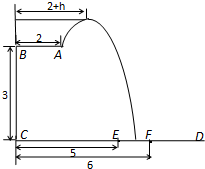
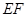 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时 ,
,
 .
. 的解集;
的解集; 的不等式
的不等式 在
在 的取值范围.
的取值范围. ,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.
,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.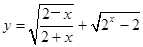 的定义域为
的定义域为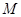 ,
, 时,求函数
时,求函数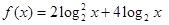 的最大值。
的最大值。 中,
中, ,点
,点 在抛物线
在抛物线 上;数列
上;数列 中,点
中,点 在过点(0, 1),以
在过点(0, 1),以 为斜率的直线上。
为斜率的直线上。 的通项公式;
的通项公式;  , 问是否存在
, 问是否存在 ,使
,使 成立,若存在,求出
成立,若存在,求出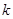 值;若不存在,说明理由;
值;若不存在,说明理由; ,不等式
,不等式 恒成立,求正数
恒成立,求正数 的取值范围。
的取值范围。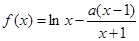 (
( ,
,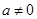 ),
), .
. 的单调区间,并确定其零点个数;
的单调区间,并确定其零点个数; 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围; (
( ).
).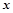 (单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当
(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当 时,车流速度v是车流密度
时,车流速度v是车流密度 时,求函数
时,求函数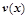 的表达式;
的表达式; 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时) %,则销售量将减少
%,则销售量将减少 %,且该化工产品每吨的价格上涨幅度不超过
%,且该化工产品每吨的价格上涨幅度不超过 %,
%, 其中
其中 为正常数
为正常数

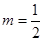 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?