题目内容
一个盒子中有2个红球和1个白球,每次取一个.
(1)若每次取出后放回,连续取两次,记A=“取出两球都是红球”,B=“第一次取出红球,第二次取出白球”,求概率P(A),P(B);
(2)若每次取出后不放回,连续取2次,记C=“取出的两球都是红球”,D=“取出的两个球中恰有1个是红球”,求概率P(C),P(D).
【答案】
(1) 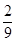 (2)
P(C)=
(2)
P(C)= 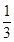 P(D)=
P(D)= 
【解析】(1) 每次取出后放回,连续取两次有9个结果,其中事件A包含4种结果,事件B包含2个结果,所以P(A)=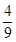 ,
P(B)=
,
P(B)=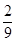 .
.
(II)要注意不放回连续取两次有6个结果.其中事件C包含2种结果,事件D包含4个结果,所以P(C)=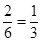 ,P(D)=
,P(D)=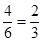 .
.
解:(1)取出后放回,连续取两次,两个红球分别记为红1和红2,列树状图如下:红1
红2 白
白 即共有9种,其中“取出两球都是红球”有4种,“第一次取出红球,第二次出
即共有9种,其中“取出两球都是红球”有4种,“第一次取出红球,第二次出
白球”有2种,
所以P(A)=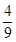 . ………………3分
. ………………3分
P(B)=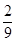 . ………………5分
. ………………5分
(2)取出后不放回,连续取两次,两个红球分别记为红1和红2,列树状图如下:
红1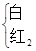 红2
红2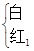 白
白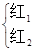 即共有6种,其中“取出两球都是红球”有2种,“取出的两个球中恰有1个是红球”有4种,
即共有6种,其中“取出两球都是红球”有2种,“取出的两个球中恰有1个是红球”有4种,
所以P(C)=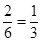 .……………………8分
.……………………8分
P(D)=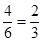 .
……………………10分
.
……………………10分

练习册系列答案
相关题目