题目内容
某篮球运动员参加了10场比赛,他每专场比赛得分的茎叶图如图所示,已知他得分的中位数为22分,若要使他得分的方差最小,则a=
2
2
,b=2
2
.
| 茎 | 叶 | |
| 1 | 2 3 3 7 | |
| 2 | a b 5 6 8 | |
| 3 | 0 | |
分析:由已知,得出a+b=4,平均分为20.8.根据方差公式,若使方差最小,只需使(20+a-20.8)2+(20+b-20.8)2最小即可.根据不等式a2+b2≥
求解即可.
| (a+b)2 |
| 2 |
解答:解:得分的中位数为22分,可知(20+a)+(20+b)=44,a+b=4,得分的和为10×4+20×5+30+(2+3+3+7)+(4+5+6+8)=208,平均分为20.8.
根据方差公式,若使方差最小,只需使(20+a-20.8)2+(20+b-20.8)2最小即可,即(a-0.8)2+(b-0.8)2最小.
根据不等式a2+b2≥
可得(a-0.8)2+(b-0.8)2≥
=2.88,当且仅当a-0.8=b-0.8,a=b=2时取到等号.
故答案为:2,2.
根据方差公式,若使方差最小,只需使(20+a-20.8)2+(20+b-20.8)2最小即可,即(a-0.8)2+(b-0.8)2最小.
根据不等式a2+b2≥
| (a+b)2 |
| 2 |
| (a+b-1.6)2 |
| 2 |
故答案为:2,2.
点评:本题考查数据的中位数,方差的概念及计算,不等式的应用.考查分析、解决、计算能力.

练习册系列答案
相关题目
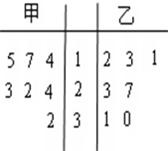 某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示 某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):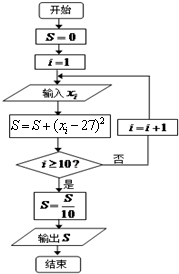 某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):