题目内容
(坐标系与参数方程)在平面直角坐标系xOy中,直线l的参数方程是
(t为参数).以O为极点,x轴正方向为极轴的极坐标系中,曲线C的极坐标方程为ρ2-2ρcosθ=0,直线l与曲线C的交点个数为
|
2
2
个.分析:化参数方程和极坐标方程为普通方程,问题转化为直线y=-x与圆(x-1)2+y2=1的交点问题,作图可得答案.
解答:解:∵直线l的参数方程是
,消去t可得直线的普通方程为y=-x,
又曲线C的极坐标方程为ρ2-2ρcosθ=0,故可得C:x2+y2-2x=0,
配方可得(x-1)2+y2=1,故曲线C表示圆,
作出它们的图象可得
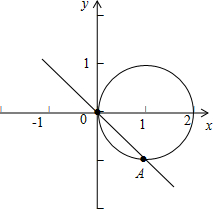
由图可知可知交点(实心点)个数为2
故答案为:2
|
又曲线C的极坐标方程为ρ2-2ρcosθ=0,故可得C:x2+y2-2x=0,
配方可得(x-1)2+y2=1,故曲线C表示圆,
作出它们的图象可得
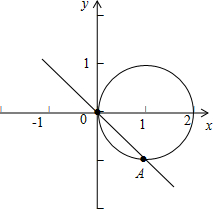
由图可知可知交点(实心点)个数为2
故答案为:2
点评:本题考查根的个数的判断,化参数方程和极坐标方程为普通方程是解决问题的关键,属中档题.

练习册系列答案
相关题目
 选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)
选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)