题目内容
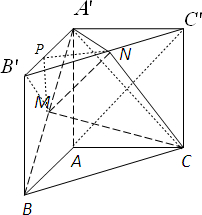
 (2012•辽宁)如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=
(2012•辽宁)如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=| 2 |
(Ⅰ)证明:MN∥平面A′ACC′;
(Ⅱ)求三棱锥A′-MNC的体积.
(椎体体积公式V=
| 1 |
| 3 |
分析:(Ⅰ)证法一,连接AB′,AC′,通过证明MN∥AC′证明MN∥平面A′ACC′.
证法二,通过证出MP∥AA′,PN∥A′C′.证出MP∥平面A′ACC′,PN∥平面A′ACC′,即能证明平面MPN∥平面A′ACC′后证明MN∥平面A′ACC′.
(Ⅱ)解法一,连接BN,则V A′-MNC=V N-A′MC=
V N-A′BC=
V A′-NBC=
.
解法二,V A′-MNC=V A′-NBC-V M-NBC=
V A′-NBC=
.
证法二,通过证出MP∥AA′,PN∥A′C′.证出MP∥平面A′ACC′,PN∥平面A′ACC′,即能证明平面MPN∥平面A′ACC′后证明MN∥平面A′ACC′.
(Ⅱ)解法一,连接BN,则V A′-MNC=V N-A′MC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
解法二,V A′-MNC=V A′-NBC-V M-NBC=
| 1 |
| 2 |
| 1 |
| 6 |
解答:(Ⅰ)(证法一)
连接AB′,AC′,由已知∠BAC=90°,AB=AC,三棱柱ABC-A′B′C′为直三棱柱,
所以M为AB′的中点,又因为N为B′C′中点,所以MN∥AC′,
又MN?平面A′ACC′,AC′?平面A′ACC′,所以MN∥平面A′ACC′;
(证法二)
取A′B′中点,连接MP,NP.而M,N分别为AB′,B′C′中点,所以MP∥AA′,PN∥A′C′.所以MP∥平面A′ACC′,PN∥平面A′ACC′;又MP∩PN=P,
所以平面MPN∥平面A′ACC′,而MN?平面MPN,所以MN∥平面A′ACC′;
(Ⅱ)(解法一)连接BN,由题意A′N⊥B′C′,平面A′B′C′∩平面B′BCC′=B′C′,所以A′N⊥平面NBC,又A′N=
B′C′=1,故
V A′-MNC=V N-A′MC=
V N-A′BC=
V A′-NBC=
.
(解法二)
V A′-MNC=V A′-NBC-V M-NBC=
V A′-NBC=
.
连接AB′,AC′,由已知∠BAC=90°,AB=AC,三棱柱ABC-A′B′C′为直三棱柱,

所以M为AB′的中点,又因为N为B′C′中点,所以MN∥AC′,
又MN?平面A′ACC′,AC′?平面A′ACC′,所以MN∥平面A′ACC′;
(证法二)
取A′B′中点,连接MP,NP.而M,N分别为AB′,B′C′中点,所以MP∥AA′,PN∥A′C′.所以MP∥平面A′ACC′,PN∥平面A′ACC′;又MP∩PN=P,
所以平面MPN∥平面A′ACC′,而MN?平面MPN,所以MN∥平面A′ACC′;
(Ⅱ)(解法一)连接BN,由题意A′N⊥B′C′,平面A′B′C′∩平面B′BCC′=B′C′,所以A′N⊥平面NBC,又A′N=
| 1 |
| 2 |
V A′-MNC=V N-A′MC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
(解法二)
V A′-MNC=V A′-NBC-V M-NBC=
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查线面关系,体积求解,考查空间想象能力、思维能力、推理论证能力、转化、计算等能力.

练习册系列答案
相关题目
 (2012•辽宁)如图,直三棱柱ABC-A'B'C',∠BAC=90°,AB=AC=λAA',点M,N分别为A'B和B'C'的中点.
(2012•辽宁)如图,直三棱柱ABC-A'B'C',∠BAC=90°,AB=AC=λAA',点M,N分别为A'B和B'C'的中点. (2012•辽宁)如图,已知椭圆C0:
(2012•辽宁)如图,已知椭圆C0: (2012•辽宁)如图,动圆
(2012•辽宁)如图,动圆