题目内容
计算:
(Ⅰ)已知x
+x-
=3,求
的值.
(Ⅱ)2•(lg
)2+
lg2•lg5+
.
(Ⅰ)已知x
| 1 |
| 2 |
| 1 |
| 2 |
x
| ||||
| x2+x-2+3 |
(Ⅱ)2•(lg
| 2 |
| 1 |
| 2 |
(lg
|
分析:(1)由于 x
+x-
=3,利用立方和公式公式求出 x
+x-
的值,再求出x2+x-2的值,代入要求的式子化简可得结果.
(2)根据有理指数幂的运算法则以及根式与分数指数幂的关系,化简要求的式子,从而求得结果.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(2)根据有理指数幂的运算法则以及根式与分数指数幂的关系,化简要求的式子,从而求得结果.
解答:解:(1)∵x
+x-
=3,∴x
+x-
=(x
+x-
)(x1+x-1-1)=(x
+x-
)((x
+x-
)2-3)= 3(9-3) =18,
又 x2+x-2=(x1+x-1)2-2=[(x
+x-
)2-2]2-2=47,
∴原式=
=
.
(2)原式=2•(
lg2)2+
lg2•lg5+
=
lg22+
lg2•lg5-(lg
-1)
=
lg22+
lg2•lg5-
lg2+1=
lg2(lg2+lg5-1)+1
=
lg2(lg10-1)+1=0+1=1.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又 x2+x-2=(x1+x-1)2-2=[(x
| 1 |
| 2 |
| 1 |
| 2 |
∴原式=
| 18+2 |
| 47+3 |
| 2 |
| 5 |
(2)原式=2•(
| 1 |
| 2 |
| 1 |
| 2 |
(lg
|
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:本题主要考查对数的运算性质、立方和公式、以及有理指数幂的运算法则的应用,属于基础题.

练习册系列答案
相关题目
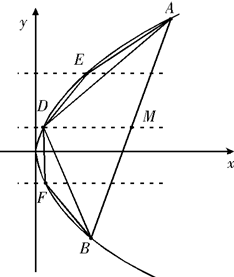 (2007•浦东新区二模)已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.
(2007•浦东新区二模)已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.