题目内容
18、给出下列命题:
①变量y与x之间的相关系数r=-0.9568,查表到相关系数的临界值为r0.05=0.8016,则变量y与x之间具有线性关系;
②a>0,b>0则不等式a3+b3≥3ab2恒成立;
③对于函数f(x)=2x2+mx+n.若f(a)>0.f(b)>0,则函数在(a,b)内至多有一个零点;
④y=f(x-2)与y=f(2-x)的图象关于x=2对称.其中所有正确命题的序号是
①变量y与x之间的相关系数r=-0.9568,查表到相关系数的临界值为r0.05=0.8016,则变量y与x之间具有线性关系;
②a>0,b>0则不等式a3+b3≥3ab2恒成立;
③对于函数f(x)=2x2+mx+n.若f(a)>0.f(b)>0,则函数在(a,b)内至多有一个零点;
④y=f(x-2)与y=f(2-x)的图象关于x=2对称.其中所有正确命题的序号是
①④
.分析:本题综合考察了相关系数,不等式的证明,函数的零点,函数的对称性,我们根据上述知识点对题目中四个结论逐一进行判断,即可得到结论.
解答:解:由相关系数的作用,当|r|越接近1,表示变量y与x之间的线性相关关系越强;
故由变量y与x之间的相关系数r=-0.9568,相关系数的临界值为r0.05=0.8016
可得变量y与x之间具有线性关系,即①正确;
当a=b=1时,a3+b3=2<3ab2=3,故a>0,b>0则不等式a3+b3≥3ab2恒成立错误;
对于函数f(x)=2x2+mx+n.若f(a)>0.f(b)>0,则函数在(a,b)内至少有一个零点,故③错误;
y=f(x-2)与y=f(2-x)的图象关于x=2对称,故④正确.
故答案为:①④
故由变量y与x之间的相关系数r=-0.9568,相关系数的临界值为r0.05=0.8016
可得变量y与x之间具有线性关系,即①正确;
当a=b=1时,a3+b3=2<3ab2=3,故a>0,b>0则不等式a3+b3≥3ab2恒成立错误;
对于函数f(x)=2x2+mx+n.若f(a)>0.f(b)>0,则函数在(a,b)内至少有一个零点,故③错误;
y=f(x-2)与y=f(2-x)的图象关于x=2对称,故④正确.
故答案为:①④
点评:相关系数|r|越接近1,表示变量y与x之间的线性相关关系越强;相关系数|r|越接近0,表示变量y与x之间的线性相关关系越弱;
函数f(x)=2x2+mx+n.若f(a)>0.f(b)>0,则函数在(a,b)内至少有一个零点.
函数f(x)=2x2+mx+n.若f(a)>0.f(b)>0,则函数在(a,b)内至少有一个零点.

练习册系列答案
相关题目
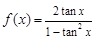 与
与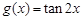 是同一个函数;②在
是同一个函数;②在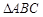 中,若
中,若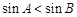 ,则
,则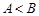 ;③
;③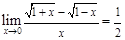 ;④随机变量
;④随机变量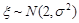 ,若
,若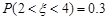 ,则
,则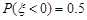 .其中正确命题的序号为
.其中正确命题的序号为 .(填所有正确命题的序号)
.(填所有正确命题的序号)