Question

求证：对角线互相垂直的四边形中，各边中点在同一个圆周上．

已知：如下图，四边形ABCD，AC⊥BD，AB、BC、CD、DA四边中点分别为E、F、G、H．

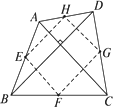
求证：E、F、G、H四点共圆．

Answer 1

答案：
解析：

证明：如上图，连结EF、FG、GH、EH． 　　因为E、F分别是AB、BC的中点， 　　所以EF是△ABC的中位线． 　　所以EF∥AC． 　　同理，EH∥BD， 　　因为AC⊥BD， 　　所以EF⊥EH， 　　即∠HEF＝90°． 　　同理，∠HGF＝90°． 　　所以∠HEF＋∠HGF＝180°． 　　所以E、F、G、H四点共圆． 　　分析：要证明此四点共圆，可以利用圆内接四边形的判定定理．