题目内容
求证：若圆内接四边形的两条对角线互相垂直，则从对角线交点到一边中点的线段长等于圆心到该边对边的距离．
[解析] 以两条对角线的交点为原点O、对角线所在直线为坐标轴建立直角坐标系．(如图所示)
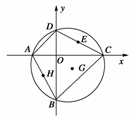
设A(－a,0)，B(0，－b)，C(c,0)，D(0，d)，
则CD的中点E
，
AB的中点H
，
又圆心G到四个顶点的距离相等，
故圆心G的横坐标等于AC中点的横坐标，
圆心G的纵坐标等于BD中点的纵坐标，
即圆心G
，∴|OE|2＝
，
|GH|2＝，∴|OE|＝|GH|，结论成立．
练习册系列答案
相关题目
为矩阵
属于λ的一个特征向量，求实数a，λ的值及A2。
（α为参数），曲线D的参数方程为
，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。