题目内容
数列{an}满足a1=1,a2=2,an+2=(1+cos2![]() )an+sin
)an+sin![]() ,n=1、2、3…
,n=1、2、3…
(1)求a3、a4并求数列{an}的通项公式
(2)设bn=![]() ,令 Sn=
,令 Sn=![]() 求 Sn
求 Sn
(1) ∴an=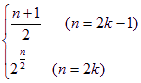 (2)Sn=2-
(2)Sn=2-![]()
解析:
(1)a3=2 a4=4
当n=2k-1时,a2k+1=a2k-1+1
∴a1,a3,a5…a2k-1…成等差数列,公差d=1
a2k-1=1+(k-1)·1=k
∴an=![]()
当n=2k时 a2k+2=2·a2k
即数列a2,a4,a6…成等比数列,公比q=2
a2k=2·2k-1=2k
∴an=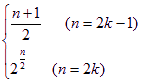
(2)bn=![]()
Sn=1![]()
由错位相减得:
Sn=2-![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
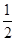 an-1+1 (n≥2)
an-1+1 (n≥2)