题目内容
设点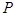 是曲线
是曲线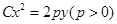 上的动点,点
上的动点,点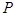 到点(0,1)的距离和它到焦点
到点(0,1)的距离和它到焦点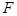 的距离之和的最小值为
的距离之和的最小值为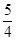 .
.
(1)求曲线C的方程;
(2)若点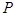 的横坐标为1,过
的横坐标为1,过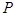 作斜率为
作斜率为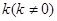 的直线交
的直线交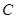 于点
于点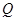 ,交
,交 轴于点
轴于点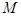 ,过点
,过点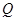 且与
且与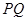 垂直的直线与
垂直的直线与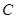 交于另一点
交于另一点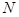 ,问是否存在实数
,问是否存在实数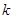 ,使得直线
,使得直线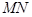 与曲线
与曲线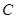 相切?若存在,求出
相切?若存在,求出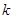 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1)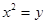 ;(2)
;(2)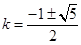 .
.
【解析】第一问中国,利用依题意知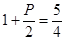 ,解得
,解得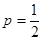 ,所以曲线
,所以曲线 的方程为
的方程为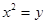
第二问中,设直线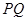 的方程为:
的方程为: ,则点
,则点 联立方程组
联立方程组 ,消去
,消去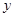 得
得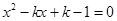
得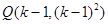 .所以得直线
.所以得直线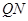 的方程为
的方程为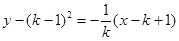 .
.
代入曲线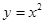 ,.解得
,.解得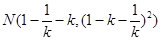
解:(Ⅰ)依题意知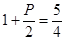 ,解得
,解得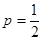 .
.
所以曲线 的方程为
的方程为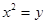 . ……………………………………………………………………4分
. ……………………………………………………………………4分
(Ⅱ)由题意直线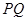 的方程为:
的方程为: ,则点
,则点
联立方程组 ,消去
,消去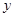 得
得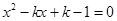 所以直线
所以直线 的斜率
的斜率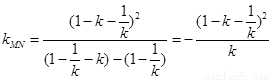 ,从而得到结论。
,从而得到结论。
得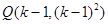 .………………………………………………………………………………6分
.………………………………………………………………………………6分
所以得直线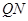 的方程为
的方程为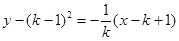 .
.
代入曲线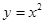 ,得
,得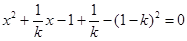 .
.
解得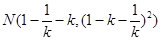 .…………………………………………………………………8分
.…………………………………………………………………8分
所以直线 的斜率
的斜率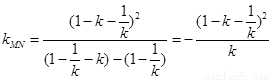 …………………………10分
…………………………10分
过点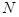 的切线的斜率
的切线的斜率 .
.
由题意有 .
.
解得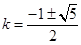 .
.
故存在实数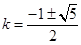 使命题成立.……………………………………………………………12分
使命题成立.……………………………………………………………12分

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(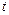 为参数),若圆
为参数),若圆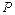 在以该直
在以该直 角坐标系的原点
角坐标系的原点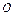 为极点、
为极点、 轴的正半轴为极轴的极坐标系下的方程为
轴的正半轴为极轴的极坐标系下的方程为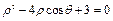
 .
.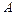 是曲线
是曲线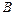 是圆
是圆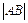 的最小值.
的最小值. 是曲线
是曲线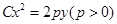 上的动点,点
上的动点,点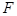 的距离之和的最小值为
的距离之和的最小值为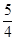 .
.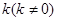 的直线交
的直线交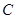 于点
于点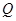 ,交
,交 轴于点
轴于点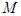 ,过点
,过点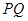 垂直的直线与
垂直的直线与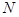 ,问是否存在实数
,问是否存在实数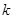 ,使得直线
,使得直线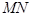 与曲线
与曲线 中,曲线
中,曲线 的参数方程为
的参数方程为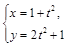 (
( 为参数),若圆
为参数),若圆 在以该直角坐标系的原点
在以该直角坐标系的原点 为极点、
为极点、 轴的正半轴为极轴的极坐标系下的方程为
轴的正半轴为极轴的极坐标系下的方程为 .
. 是曲线
是曲线 是圆
是圆 的最小值.
的最小值.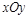 中,曲线
中,曲线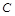 的参数方程为
的参数方程为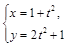 (
(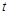 为参数),若圆
为参数),若圆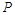 在以该直角坐标系的原点
在以该直角坐标系的原点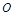 为极点、
为极点、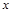 轴的正半轴为极轴的极坐标系下的方程为
轴的正半轴为极轴的极坐标系下的方程为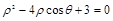 .
.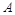 是曲线
是曲线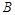 是圆
是圆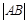 的最小值.
的最小值.