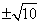题目内容
已知函数 的最大值为2.
的最大值为2.(1)求函数f(x)在[0,π]上的单调递减区间;
(2)△ABC中,
 ,角A,B,C所对的边分别是a,b,c,且C=60°,c=3,求△ABC的面积.
,角A,B,C所对的边分别是a,b,c,且C=60°,c=3,求△ABC的面积.
【答案】分析:(1)将f(x)解析式利用两角和与差的正弦函数公式化为一个角的正弦函数,由正弦函数的值域表示出f(x)的最大值,由已知最大值为2列出关于m的方程,求出方程的解得到m的值,进而确定出f(x)的解析式,由正弦函数的递减区间为[2kπ+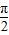 ,2kπ+
,2kπ+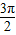 ](k∈Z),列出关于x的不等式,求出不等式的解集即可得到f(x)在[0,π]上的单调递减区间;
](k∈Z),列出关于x的不等式,求出不等式的解集即可得到f(x)在[0,π]上的单调递减区间;
(2)由(1)确定的f(x)解析式化简f(A-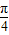 )+f(B-
)+f(B-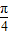 )=4
)=4 sinAsinB,再利用正弦定理化简,得出a+b=
sinAsinB,再利用正弦定理化简,得出a+b=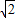 ab①,利用余弦定理得到(a+b)2-3ab-9=0②,将①代入②求出ab的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.
ab①,利用余弦定理得到(a+b)2-3ab-9=0②,将①代入②求出ab的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.
解答:解:(1)f(x)=msinx+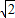 cosx=
cosx=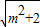 sin(x+θ)(其中sinθ=
sin(x+θ)(其中sinθ= ,cosθ=
,cosθ=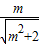 ),
),
∴f(x)的最大值为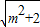 ,
,
∴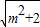 =2,
=2,
又m>0,∴m=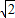 ,
,
∴f(x)=2sin(x+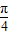 ),
),
令2kπ+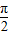 ≤x+
≤x+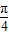 ≤2kπ+
≤2kπ+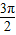 (k∈Z),解得:2kπ+
(k∈Z),解得:2kπ+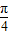 ≤x≤2kπ+
≤x≤2kπ+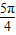 (k∈Z),
(k∈Z),
则f(x)在[0,π]上的单调递减区间为[ ,π];
,π];
(2)设△ABC的外接圆半径为R,由题意C=60°,c=3,得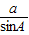 =
= =
=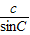 =
= =2
=2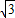 ,
,
化简f(A-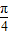 )+f(B-
)+f(B- )=4
)=4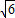 sinAsinB,得sinA+sinB=2
sinAsinB,得sinA+sinB=2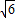 sinAsinB,
sinAsinB,
由正弦定理得: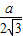 +
+ =2
=2 ×
×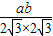 ,即a+b=
,即a+b=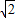 ab①,
ab①,
由余弦定理得:a2+b2-ab=9,即(a+b)2-3ab-9=0②,
将①式代入②,得2(ab)2-3ab-9=0,
解得:ab=3或ab=- (舍去),
(舍去),
则S△ABC= absinC=
absinC=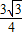 .
.
点评:此题考查了正弦、余弦定理,三角形的面积公式,两角和与差的正弦函数公式,以及正弦函数的单调性,熟练掌握定理及公式是解本题的关键.
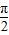 ,2kπ+
,2kπ+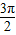 ](k∈Z),列出关于x的不等式,求出不等式的解集即可得到f(x)在[0,π]上的单调递减区间;
](k∈Z),列出关于x的不等式,求出不等式的解集即可得到f(x)在[0,π]上的单调递减区间;(2)由(1)确定的f(x)解析式化简f(A-
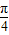 )+f(B-
)+f(B-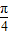 )=4
)=4 sinAsinB,再利用正弦定理化简,得出a+b=
sinAsinB,再利用正弦定理化简,得出a+b=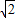 ab①,利用余弦定理得到(a+b)2-3ab-9=0②,将①代入②求出ab的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.
ab①,利用余弦定理得到(a+b)2-3ab-9=0②,将①代入②求出ab的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.解答:解:(1)f(x)=msinx+
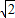 cosx=
cosx=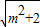 sin(x+θ)(其中sinθ=
sin(x+θ)(其中sinθ= ,cosθ=
,cosθ=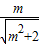 ),
),∴f(x)的最大值为
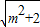 ,
,∴
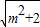 =2,
=2,又m>0,∴m=
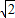 ,
,∴f(x)=2sin(x+
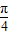 ),
),令2kπ+
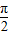 ≤x+
≤x+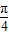 ≤2kπ+
≤2kπ+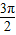 (k∈Z),解得:2kπ+
(k∈Z),解得:2kπ+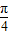 ≤x≤2kπ+
≤x≤2kπ+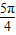 (k∈Z),
(k∈Z),则f(x)在[0,π]上的单调递减区间为[
 ,π];
,π];(2)设△ABC的外接圆半径为R,由题意C=60°,c=3,得
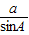 =
= =
=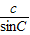 =
= =2
=2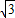 ,
,化简f(A-
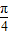 )+f(B-
)+f(B- )=4
)=4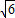 sinAsinB,得sinA+sinB=2
sinAsinB,得sinA+sinB=2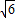 sinAsinB,
sinAsinB,由正弦定理得:
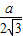 +
+ =2
=2 ×
×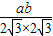 ,即a+b=
,即a+b=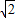 ab①,
ab①,由余弦定理得:a2+b2-ab=9,即(a+b)2-3ab-9=0②,
将①式代入②,得2(ab)2-3ab-9=0,
解得:ab=3或ab=-
 (舍去),
(舍去),则S△ABC=
 absinC=
absinC=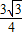 .
.点评:此题考查了正弦、余弦定理,三角形的面积公式,两角和与差的正弦函数公式,以及正弦函数的单调性,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目

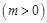 的最大值为2.
的最大值为2. 在
在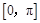 上的值域;
上的值域;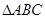 外接圆半径
外接圆半径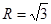 ,
,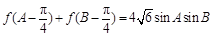 ,角A,B所对的边分别是a,b,求
,角A,B所对的边分别是a,b,求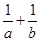 的值.
的值. 的最大值为2,则
的最大值为2,则 的最小正周期为
的最小正周期为 B.
B. C.
C. D.
D.
 的最大值为2,求实数a的值.
的最大值为2,求实数a的值.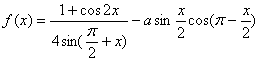 的最大值为2,则常数a的值为
的最大值为2,则常数a的值为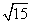 B.
B.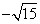 C.
C.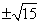 D.
D.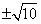
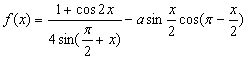 的最大值为2,则常数a的值为( )
的最大值为2,则常数a的值为( )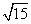 B.
B.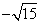 C.
C.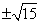 D.
D.