题目内容
（2009•宜春一模）已知方程f（x）=x2+ax+2b的两根分别在（0，1），（1，2）内，则f（3）的取值范围（ ）
分析：由题意可得
，化简可得
．目标函数z=f（3）=3a+2b+9．
画出可行域，求出目标函数的最优解，可得f（3）的取值范围．
|
|
画出可行域，求出目标函数的最优解，可得f（3）的取值范围．
解答：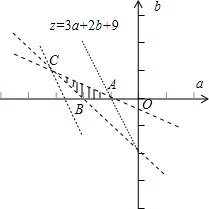
解：由题意可得
，
化简可得
．
目标函数z=f（3）=3a+2b+9．
画出可行域如图阴影部分（三角形ABC内部区域）所示：
显然，A（-1，0）、A（-3，1）为最优解．
把点C的坐标代入目标函数求得 z=2，
把点A（-1，0）代入目标函数求得 z=6，
故f（3）的范围是（2，6），
故选 B．
解：由题意可得
|
化简可得
|
目标函数z=f（3）=3a+2b+9．
画出可行域如图阴影部分（三角形ABC内部区域）所示：
显然，A（-1，0）、A（-3，1）为最优解．
把点C的坐标代入目标函数求得 z=2，
把点A（-1，0）代入目标函数求得 z=6，
故f（3）的范围是（2，6），
故选 B．
点评：本题主要考查一元二次方程根的分步与系数的关系，简单的线性规划问题，属于中档题．
练习册系列答案
相关题目