题目内容
已知函数 ,正实数
,正实数 满足
满足 ,且
,且 ,若
,若 在区间
在区间 上的最大值为2,则
上的最大值为2,则 的值为( )
的值为( )
A. | B. | C. | D. |
B
解析试题分析:∵f(x)=|log2x|,且f(m)=f(n),正实数 满足
满足 ,∴mn=1
,∴mn=1
∵若f(x)在区间[m2,n]上的最大值为2,∴|log2m2|=2,∵m<n,,∴m= ,∴n=2,∴n+m=
,∴n=2,∴n+m= ,
,
故答案为选B.
考点:本题主要考查了对数函数的图象和性质,特别是取绝对值后考查的特别多,解决的方法多数用数形结合法.
点评:解决该试题的关键是先结合函数f(x)=|log2x|的图象和性质,再由f(m)=f(n),得到m,n的倒数关系,再由“若f(x)在区间[m2,n]上的最大值为2”,求得m.n的值得到结果

练习册系列答案
相关题目
若 ,则
,则 的定义域为
的定义域为
A. | B. | C. | D. |
在区间 上为增函数的是( )
上为增函数的是( )
A. | B. |
C. | D. |
函数 的定义域是( ).
的定义域是( ).
A. | B. | C. | D. |
函数f(x)=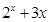 的零点所在的一个区间是
的零点所在的一个区间是
| A.(-2,-1) | B.(-1,0) | C.(0,1) | D.(1,2) |
已知函数 的图象如图所示,则
的图象如图所示,则 满足的关系是( )
满足的关系是( )
A. | B.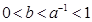 |
C. | D. |
 与
与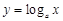 的图象可能是( )
的图象可能是( )
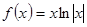 的大致图象是
的大致图象是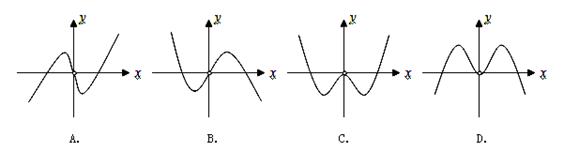
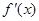 是函数
是函数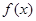 的导函数,将
的导函数,将 和
和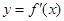 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )