题目内容

抛物线y2=2px与直线ax+y-4=0交于两点A、B,且点A的坐标是(1,2),设抛物线的焦点为F,则|FA|+|FB|等于(    )

A.7          B.3          C.6            D.5

A


解析:

由题意可求得抛物线方程为y2=4x,直线方程为2x+y-4=0.

由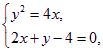得x2-5x+4=0.

设此方程的两根为x1、x2,则x1+x2=5,|FA|+|FB|=(x1+1)+(x2+1)=(x1+x2)+2=5+2=7.

练习册系列答案
相关题目
抛物线y2=2px与直线ax+y-4=0交于A、B两点，其中点A的坐标为（1，2），设抛物线的焦点为F，则|FA|+|FB|等于（　　）
A、7
B、3
5
C、6
D、5
抛物线y2=2px与直线ax+y-4=0交于A，B两点，其中A点的坐标是（1，2），该抛物线的焦点为F，则|FA+FB|=（　　）
（2011•焦作一模）已知双曲线
x2
4
-
y2
12
=1的离心率为e，焦点为F的抛物线y2=2px与直线y=k（x-
p
2
）交于A、B两点，且
|AF|
|FB|
=e，则k的值为
+
.
2
2
+
.
2
2
．

抛物线y2=2px与直线ax+y-4=0交于两点A、B,其中点A的坐标为(1,2),设抛物线的焦点为F,则|FA|+|FB|等于(    )

A.7                     B.3             C.6                 D.5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网