题目内容
若圆![]() 过点
过点![]() 且与直线
且与直线![]() 相切,设圆心
相切,设圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,
,![]() 、
、![]() 为曲线
为曲线![]() 上的两点,点
上的两点,点![]() ,且满足
,且满足![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,过
,过![]() 、
、![]() 两点的圆
两点的圆![]() 与抛物线在点
与抛物线在点![]() 处有共同的切线,求圆
处有共同的切线,求圆![]() 的方程;
的方程;
(3)分别过![]() 、
、![]() 作曲线
作曲线![]() 的切线,两条切线交于点
的切线,两条切线交于点![]() ,若点
,若点![]() 恰好在直线
恰好在直线![]() 上,求证:
上,求证:![]() 与
与![]() 均为定值.
均为定值.
21.解:(1)依题意,点![]() 到定点
到定点![]() 的距离等于到定直线
的距离等于到定直线![]() 的距离,所以点
的距离,所以点![]() 的轨迹为抛物线,曲线
的轨迹为抛物线,曲线![]() 的方程为
的方程为![]() ; …………………………………………………………3分
; …………………………………………………………3分
(2)直线![]() 的方程是
的方程是![]() ,即
,即![]() ,
,
由![]() 得点
得点![]() 、
、![]() 的坐标是
的坐标是![]() 或
或![]() ,………………………………5分
,………………………………5分
当![]() 、
、![]() 时,由
时,由![]() 得
得![]() ,
,![]() ,
,
所以抛物线![]() 在点
在点![]() 处切线的斜率为
处切线的斜率为![]() ,
,
直线![]() 的方程为
的方程为![]() ,即
,即![]() …………①
…………①
线段![]() 的中点坐标为
的中点坐标为![]() ,中垂线方程为
,中垂线方程为![]() ,即
,即![]() …………②
…………②
由①、②解得![]() , …………………………………………………………7分
, …………………………………………………………7分
于是,圆![]() 的方程为
的方程为![]() ,
,
即 ![]() , ………………………………………………………8分
, ………………………………………………………8分
当![]() 、
、![]() 时,抛物线
时,抛物线![]() 在点
在点![]() 处切线的斜率为
处切线的斜率为![]() ,此时切线与
,此时切线与![]() 垂直,所求圆为以
垂直,所求圆为以![]() 为直径的圆,可求得圆为
为直径的圆,可求得圆为![]() , ……9分
, ……9分
(3)设![]() ,
,![]() ,
,![]() ,过点
,过点![]() 的切线方程为
的切线方程为![]() ,
,
即![]() ,同理可得
,同理可得![]() ,所以
,所以![]() ,
,![]() ,……10分
,……10分
又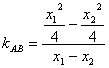 =
=![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
即![]() ,亦即
,亦即![]() ,所以
,所以![]() ,………………………………………11分
,………………………………………11分
而![]() ,
,![]() ,所以
,所以
![]()
![]()
![]() . …………………………………13分
. …………………………………13分

练习册系列答案
相关题目
 过点
过点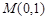 且与直线
且与直线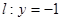 相切,设圆心
相切,设圆心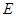 ,
, 、
、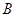 为曲线
为曲线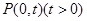 ,且满足
,且满足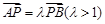 .
.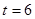 ,直线
,直线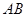 的斜率为
的斜率为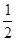 ,过
,过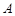 、
、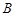 两点的圆
两点的圆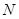 与抛物线在点
与抛物线在点 ,若点
,若点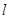 上,求证:
上,求证: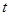 与
与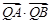 均为定值.
均为定值. 且与直线
且与直线 相切.
相切. 与轨迹E交于点A、B,M是线段AB的中点,过M作
与轨迹E交于点A、B,M是线段AB的中点,过M作 轴的垂线交轨迹E于N.
轴的垂线交轨迹E于N. 与AB平行;
与AB平行;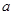 ,使
,使 ?若存在,求
?若存在,求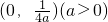 且与直线
且与直线 相切.
相切.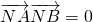 ?若存在,求a的值;若不存在,说明理由.
?若存在,求a的值;若不存在,说明理由.