题目内容
若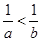 ,则在下列不等式:①
,则在下列不等式:①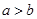 ;②
;② ;③
;③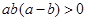 ;④
;④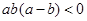 中,可以成立的不等式的个数为
中,可以成立的不等式的个数为
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析: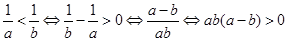 。故③必然成立,④一定不会成立。若
。故③必然成立,④一定不会成立。若 ,则
,则 ,②可以成立。若
,②可以成立。若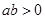 ,则
,则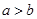 ,①也可以成立。选C。
,①也可以成立。选C。
考点:本题主要考查不等式的基本性质。
点评:不等式性质的应用比较繁杂,应注意从基本的不等式成立入手,推断出相关结论。

练习册系列答案
相关题目
设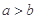 ,
,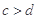 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.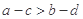 | B.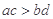 | C.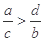 | D.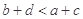 |
定义区间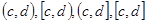 的长度均为
的长度均为 ,其中
,其中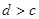 ,已知实数
,已知实数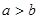 ,则满足
,则满足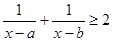 的x构成的区间长度之和为( )
的x构成的区间长度之和为( )
| A.1 | B.a-b | C.a+b | D.2 |
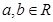 ,下列命题正确的是( )
,下列命题正确的是( )
A.若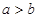 ,则 ,则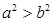 | B.若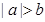 ,则 ,则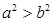 |
C.若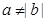 ,则 ,则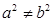 | D.若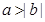 ,则 ,则 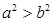 |
给出下列不等式:①a2+1≥2a;②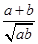 ≥2;③x2+
≥2;③x2+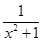 ≥1.其中正确的个数是( )
≥1.其中正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
若a、b、c∈R,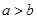 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.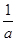 < <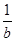 | B. |
C.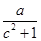 > >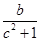 | D. |
给出下列命题,其中正确的是( )
A.若 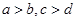 ,则 ,则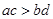 ; ; | B.若 ,则 ,则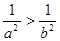 ; ; |
C.若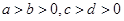 ,则 ,则 ; ; | D.若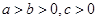 ,则 ,则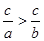 . . |
若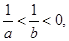 则下列不等式:①
则下列不等式:① ;②
;②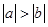 ;③
;③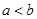 ;④
;④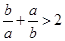 中正确的是( )
中正确的是( )
| A.①② | B.②③ | C.①④ | D.③④ |
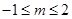 ,则
,则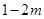 的取值范围是____________。
的取值范围是____________。