题目内容
设F1、F2分别为椭圆C: =1(a>b>0)的左、右两个焦 点。(1)若椭圆C上的点A(1,
=1(a>b>0)的左、右两个焦 点。(1)若椭圆C上的点A(1, )到F1、F2两点的 距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的 距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程.
【答案】
(1)椭圆C的方程为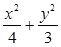 =1,焦点F1(-1,0),F2(1,0);(2)
=1,焦点F1(-1,0),F2(1,0);(2)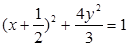
【解析】
试题分析:(1)椭圆C的焦点在x轴上,
由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a="2." (2分)
又点A(1,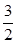 )在椭圆上,因此
)在椭圆上,因此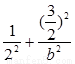 =1得b2=3,于是c2="1."
(4分)
=1得b2=3,于是c2="1."
(4分)
所以椭圆C的方程为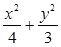 =1,焦点F1(-1,0),F2(1,0)
(6分)
=1,焦点F1(-1,0),F2(1,0)
(6分)
(2)设椭圆C上的动点为K(x1, y1),线段F1K的中点Q(x,y)满足:
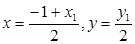 , 即x1=2x+1,y1=2y. (10分)
, 即x1=2x+1,y1=2y. (10分)
代入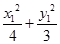 =1得
=1得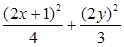 =1.
=1.
即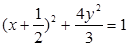 为所求的轨迹方程. (14分)
为所求的轨迹方程. (14分)
考点:本题考查了椭圆方程的求法及轨迹方程的求法
点评:处理轨迹问题时往往用到以下要注意用到这个方法:(1)结合解析几何中某种曲线的定义,从定义出发寻找解决问题的方法;(2)利用几何性质,若所求的轨迹与图形的性质相关,往往利用三角形或圆的性质来解问题;(3)如果点P的运动轨迹或所在曲线已知,又点Q与点P之间的坐标可以建立某种关系,则借助点P的轨迹可以得到点Q的轨迹;(4)参数法

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点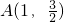 到两点的距离之和等于4.
到两点的距离之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.