题目内容
已知a=( ,-1),b=
,-1),b= .
.
(1)求证:a⊥b;
(2)若存在不同时为0的实数k和t,使x=a+(t-3)b,y=-ka+tb,且x⊥y,试求函数关系式k=f(t);
(3)求函数k=f(t)的最小值.
【答案】
(1)见解析(2)k=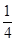 t(t-3).(3)-
t(t-3).(3)-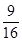 .
.
【解析】 (1)由a·b=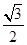 -
-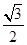 =0,得a⊥b.
=0,得a⊥b.
(2)由x⊥y得,x·y=[a+(t-3)b]·(-ka+tb)=0,即-ka2-k(t-3)a·b+ta·b+t(t-3)b2=0.
-ka2+t(t-3)b2=0.
∴k=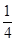 t(t-3).
t(t-3).
(3)k=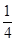 t(t-3)=
t(t-3)=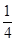
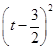 -
-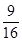 ,
,
所以当t=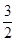 时,k取最小值-
时,k取最小值-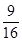 .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目