题目内容
一个袋子里装有编号为1,2,3,4,5的5个大小形状均相同的小球,从中任取两个小球.(I)请列举出所有可能的结果;
(II)求两球编号之差的绝对值小于2的概率.
【答案】分析:(Ⅰ)由题意列举可得可能结果;(Ⅱ)由(Ⅰ)知,所有可能结果共10种,符合题意得包含(1,2),(2,3),(3,4),(4,5)四种结果,由古典概型的概率公式可得答案.
解答:解:(Ⅰ)由题意可得所有可能结果为(1,2),(1,3),(1,4),(1,5),
(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)…(6分)
(Ⅱ)由(Ⅰ)知,所有可能结果共10种,设两球编号之差的绝对值为X,
则X的值只能为1,包含(1,2),(2,3),(3,4),(4,5)四种结果.…(8分)
故所求的概率为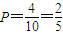 …(11分)
…(11分)
故所求两球编号之差的绝对值小于2的概率为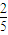 .…(12分)
.…(12分)
点评:本题考查列举法计算基本事件数及事件发生的概率,属基础题.
解答:解:(Ⅰ)由题意可得所有可能结果为(1,2),(1,3),(1,4),(1,5),
(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)…(6分)
(Ⅱ)由(Ⅰ)知,所有可能结果共10种,设两球编号之差的绝对值为X,
则X的值只能为1,包含(1,2),(2,3),(3,4),(4,5)四种结果.…(8分)
故所求的概率为
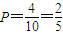 …(11分)
…(11分)故所求两球编号之差的绝对值小于2的概率为
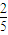 .…(12分)
.…(12分)点评:本题考查列举法计算基本事件数及事件发生的概率,属基础题.

练习册系列答案
相关题目