题目内容
已知双曲线的两条渐近线方程为直线l1:y=
x和l2:y=-
x,其焦点在x轴上,实轴长为2.
(Ⅰ)求双曲线的方程;
(Ⅱ)设直线l:y=kx+1与双曲线相切于点M且与右准线交于N,F为右焦点,求证:∠MFN为直角.
| 3 |
| 3 |
(Ⅰ)求双曲线的方程;
(Ⅱ)设直线l:y=kx+1与双曲线相切于点M且与右准线交于N,F为右焦点,求证:∠MFN为直角.
分析:(Ⅰ)设出双曲线的方程,根据焦点在x轴上,实轴长为2,求出参数,即可求双曲线的方程;
(Ⅱ)由y=kx+1代入双曲线方程,消去y,利用△=0,求出k的值,进而求出M,N的坐标,即可证明结论.
(Ⅱ)由y=kx+1代入双曲线方程,消去y,利用△=0,求出k的值,进而求出M,N的坐标,即可证明结论.
解答:(Ⅰ)解:由题意,设双曲线方程为 3x2-y2=λ(λ>0)⇒
-
=1.
又2a=1,∴a=1,
∴
=1,∴λ=3,
∴方程为x2-
=1;
(Ⅱ)证明:由y=kx+1代入双曲线方程,消去y得(3-k2)x2-2kx-4=0,
由
,可得
,
∴k=±2,
当k=2时得 xM=-2,代入y=2x+1得yM=-3,
∴M(-2,-3),
由
⇒N(
,2),
∴F(2,0)⇒
=(-4,-3),
=(-
,2)⇒
•
=6-6=0⇒
⊥
;
当k=-2时同理得M(2,-3),N(
,0),F(2,0)⇒
=(0,-3),
=(-
,0)⇒
•
=0⇒
⊥
,
综上:∠MFN为直角.
| x2 | ||
|
| y2 |
| λ |
又2a=1,∴a=1,
∴
|
∴方程为x2-
| y2 |
| 3 |
(Ⅱ)证明:由y=kx+1代入双曲线方程,消去y得(3-k2)x2-2kx-4=0,
由
|
|
∴k=±2,
当k=2时得 xM=-2,代入y=2x+1得yM=-3,
∴M(-2,-3),
由
|
| 1 |
| 2 |
∴F(2,0)⇒
| FM |
| FN |
| 3 |
| 2 |
| FM |
| FN |
| FM |
| FN |
当k=-2时同理得M(2,-3),N(
| 1 |
| 2 |
| FM |
| FN |
| 3 |
| 2 |
| FM |
| FN |
| FM |
| FN |
综上:∠MFN为直角.
点评:本题考查双曲线的方程,考查直线与双曲线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,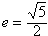 。
。