题目内容
13．已知向量$\overrightarrow{a}$=（-2，1），$\overrightarrow{b}$=（x，y），x∈[1，6]，y∈[1，6]则满足$\overrightarrow{a}$•$\overrightarrow{b}$＜0的概率是（ ）| A． | $\frac{21}{25}$ | B． | $\frac{23}{25}$ | C． | $\frac{1}{5}$ | D． | $\frac{3}{25}$ |
分析 可用A表示事件“$\overrightarrow{a}•\overrightarrow{b}＜0$”，可以得到试验的全部结果所构成的区域为{（x，y）|1≤x≤6，1≤y≤6}，而事件A表示的区域为{（x，y）|1≤x≤6，1≤y≤6，-2x+y＜0}，从而可画图表示这两个区域，从而求这两个区域的面积比便是事件A的概率．
解答 解：用A表示事件“$\overrightarrow{a}•\overrightarrow{b}＜0$”；
试验的全部结果所构成的区域为{（x，y）|1≤x≤6，1≤y≤6}；
构成事件A的区域为{（x，y）|1≤x≤6，1≤y≤6，且-2x+y＜0}；
画出图形如下图：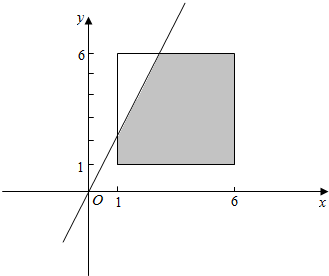
图中矩形及矩形内部表示试验的全部结果所表示的区域，阴影部分表示事件A表示的区域；
∴P（A）=$\frac{5×5-\frac{1}{2}×4×2}{5×5}=\frac{21}{25}$．
故选：A．
点评 考查概率的概念，几何概型的计算方法，以及能够找出不等式所表示的平面区域．
练习册系列答案
天天练口算系列答案
相关题目
函数f（x）=$\sqrt{2}$sin（ωx+φ）（x∈R，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的解析式为f（x）=$\sqrt{2}$sin（2x+$\frac{π}{6}$）；f（x）的图象的横坐标缩小为原来的$\frac{1}{2}$后得函数y=g（x）的图象，则g（x）的单调减区间为[$\frac{π}{12}$+$\frac{1}{2}$kπ，$\frac{π}{3}$+$\frac{1}{2}$kπ]，k∈Z．
4．点A，B，C，D均在同一球面上，且AB，AC，AD两两垂直，且AB=1，AC=2，AD=3，则该球的表面积为（ ）
| A． | 7π | B． | 14π | C． | $\frac{7}{2}π$ | D． | $\frac{{7\sqrt{14}π}}{3}$ |
18．已知f（x）=x5-ax3+bx+2，且f（-5）=3，则f（5）+f（-5）的值为（ ）
| A． | 0 | B． | 4 | C． | 6 | D． | 1 |