题目内容
椭圆上一点P(2,1)到两焦点F1、F2的距离之和是焦距的两倍,求椭圆的标准方程.
解:若椭圆焦点在x轴上,方程为![]() +
+![]() =1(a>b>0),由题意得
=1(a>b>0),由题意得
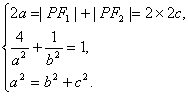
解得a2=![]() ,b2=4.
,b2=4.
此时椭圆方程为![]() +
+![]() =1.
=1.
若焦点在y轴上,设方程为![]() +
+![]() =1(a>b>0).
=1(a>b>0).
由题意,得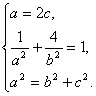
解之,得a2=![]() ,b2=
,b2=![]() .
.
此时椭圆方程为![]() +
+![]() =1.
=1.
综上,知所求椭圆方程为![]() +
+![]() =1或
=1或![]() +
+![]() =1.
=1.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
题目内容
椭圆上一点P(2,1)到两焦点F1、F2的距离之和是焦距的两倍,求椭圆的标准方程.
解:若椭圆焦点在x轴上,方程为![]() +
+![]() =1(a>b>0),由题意得
=1(a>b>0),由题意得
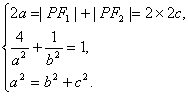
解得a2=![]() ,b2=4.
,b2=4.
此时椭圆方程为![]() +
+![]() =1.
=1.
若焦点在y轴上,设方程为![]() +
+![]() =1(a>b>0).
=1(a>b>0).
由题意,得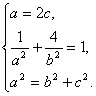
解之,得a2=![]() ,b2=
,b2=![]() .
.
此时椭圆方程为![]() +
+![]() =1.
=1.
综上,知所求椭圆方程为![]() +
+![]() =1或
=1或![]() +
+![]() =1.
=1.

 计算高手系列答案
计算高手系列答案