题目内容
设椭圆M: (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4。
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4。
(1)求椭圆M的方程;
(2)若直线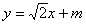 交椭圆于A,B两点,椭圆上一点P(1,
交椭圆于A,B两点,椭圆上一点P(1,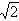 ),求△PAB面积的最大值。
),求△PAB面积的最大值。
 (a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4。
(a>b>0)的离心率与双曲线x2-y2=1的离心率互为倒数,且内切于圆x2+y2=4。(1)求椭圆M的方程;
(2)若直线
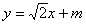 交椭圆于A,B两点,椭圆上一点P(1,
交椭圆于A,B两点,椭圆上一点P(1,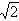 ),求△PAB面积的最大值。
),求△PAB面积的最大值。解:(1)双曲线的离心率为
则椭圆的离心率为
圆x2+y2=4的直径为4,则2a=4
得
所求椭圆M的方程为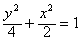 。
。
(2)直线AB的直线方程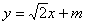
由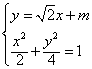 得
得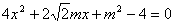
由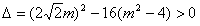
得
∵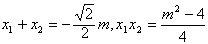
∴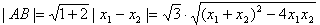
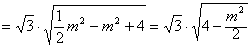
又P到AB的距离为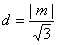
则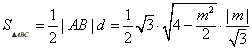
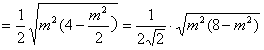
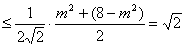
当且仅当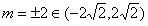 时取等号
时取等号
∴ 。
。

则椭圆的离心率为

圆x2+y2=4的直径为4,则2a=4
得

所求椭圆M的方程为
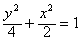 。
。(2)直线AB的直线方程
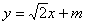
由
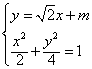 得
得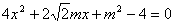
由
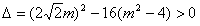
得

∵
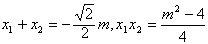
∴
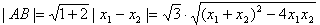
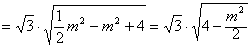
又P到AB的距离为
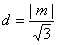
则
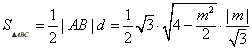
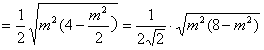
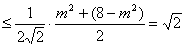
当且仅当
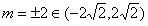 时取等号
时取等号∴
 。
。
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
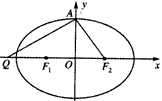
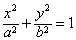 (a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且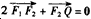 。
。
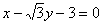 相切,求椭圆C的方程;
相切,求椭圆C的方程;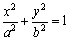 (a > b > 0)过M(2,
(a > b > 0)过M(2,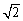 ),N(
),N(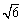 ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,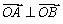 ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求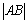 取值范围;若不存在,说明理由.
取值范围;若不存在,说明理由.