题目内容
16．
已知函数f（x）是定义在R上的奇函数，且当x≤0时，f（x）=x2+2x，函数f（x）在y轴左侧的图象如图所示．（1）补全f（x）的图象，并写出函数的单调区间；
（2）若函数g（x）=af（x）-2ax+2，x∈[1，2]，求函数g（x）的最小值．
分析 （1）根据奇函数图象的对称性，补全f（x）的图象，并写出函数的单调区间；
（2）利用函数的奇偶性和已知的x≤0时解析式，求出函数在x＞0时的解析式，得到函数g（x）的解析式，再通过分类讨论研究二次函数在区间上的值域，得到本题结论．
解答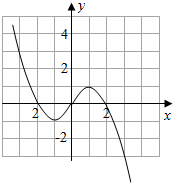 
解：（1）图象如图所示，
函数的单调增区间是（-1，1），单调减区间是（-∞，-1），（1，+∞）；
（2）∵函数f（x）是定义在R上的奇函数，
∴f（-x）=-f（x）．
∵当x≤0时，f（x）=x2+2x，
∴当x＞0时，-x＜0，
f（x）=-f（-x）=-[（-x）2+（-x）]=-x2+2x，
∵函数g（x）=f（x）-2ax+2，x∈[1，2]，
∴g（x）=-ax2+2，x∈[1，2]，
当a＜0时，[g（x）]min=g（2）=-4a+2；
当a＞0时，[g（x）]min=g（1）=-a+2．
∴[g（x）]min=$\left\{\begin{array}{l}{-4a+2，a＜0}\\{-a+2，a＞0}\end{array}\right.$．
点评 本题考查了函数的奇偶性、函数解析式、二次函数在区间上的值域，本题难度不大，属于中档题．
练习册系列答案
新思维寒假作业系列答案
相关题目