题目内容
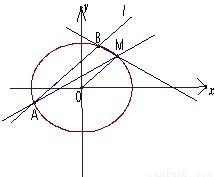
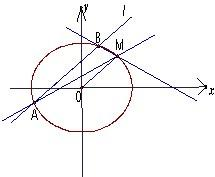 如图,已知椭圆C过点M(2,1),两个焦点分别为(-
如图,已知椭圆C过点M(2,1),两个焦点分别为(-| 6 |
| 6 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)试问直线MA、MB的斜率之和是否为定值,若为定值,求出以线段AB为直径且过点M的圆的方程;若不存在,说明理由.
分析:(Ⅰ)由题设知半焦距c=
,长半轴长a=
=
=2
,短半轴长b=
=
,由此能得到椭圆C的方程.
(Ⅱ)设直线l的方程为y=
x+m,A(x1,y1),B(x2,y2),kMA=
=
=
+
,kMB=
+
,由
知x2+2mx+2m2-4=0,得x1+x2=-2m,x1x2=2m2-4.由此入手能够求出圆的方程.
| 6 |
| ||||||||
| 2 |
| ||||||||||
| 2 |
| 2 |
(2
|
| 2 |
(Ⅱ)设直线l的方程为y=
| 1 |
| 2 |
| y1-1 |
| x1-2 |
| ||
| x1-2 |
| 1 |
| 2 |
| m |
| x1-2 |
| 1 |
| 2 |
| m |
| x2-2 |
|
解答:解:(Ⅰ)由题设知:半焦距c=
,
长半轴长a=
=
=2
,
短半轴长b=
=
,于是椭圆C的方程是:
+
=1;
(Ⅱ)设直线l的方程为y=
x+m,A(x1,y1),B(x2,y2)kMA=
=
=
+
,kMB=
+
由
知x2+2mx+2m2-4=0,得x1+x2=-2m,x1x2=2m2-4;
∴kMA+kMB=1+
=1+
=0为定值;
由线段AB为直径且过点M的圆知:MA⊥MB有kMA•kMB=-1,得kMA=1,kMB=-1;
∴
+
=1,
+
=-1,又x1+x2=-2m;得x1=-
,x2=
;
∴y1=-
,y2=
,圆的方程为:(x+
)(x-
)+(y+
)(y-
)=0
即:(x-
)2+(y+
)2=
.
| 6 |
长半轴长a=
| ||||||||
| 2 |
| ||||||||||
| 2 |
| 2 |
短半轴长b=
(2
|
| 2 |
| x2 |
| 8 |
| y2 |
| 2 |
(Ⅱ)设直线l的方程为y=
| 1 |
| 2 |
| y1-1 |
| x1-2 |
| ||
| x1-2 |
| 1 |
| 2 |
| m |
| x1-2 |
| 1 |
| 2 |
| m |
| x2-2 |
由
|
∴kMA+kMB=1+
| m(x1+x2-4) |
| x1x2-2(x1+x2)+4 |
| m(-2m-4) |
| 2m2-4-2(-2m)+4 |
由线段AB为直径且过点M的圆知:MA⊥MB有kMA•kMB=-1,得kMA=1,kMB=-1;
∴
| 1 |
| 2 |
| m |
| x1-2 |
| 1 |
| 2 |
| m |
| x2-2 |
| 2 |
| 5 |
| 14 |
| 5 |
∴y1=-
| 7 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 14 |
| 5 |
| 7 |
| 5 |
| 1 |
| 5 |
即:(x-
| 6 |
| 5 |
| 3 |
| 5 |
| 16 |
| 5 |
点评:本题考查椭圆方程的求法和圆与直线位置关系的综合运用,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
相关题目
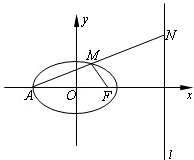 如图,已知椭圆
如图,已知椭圆 如图,已知椭圆C:
如图,已知椭圆C: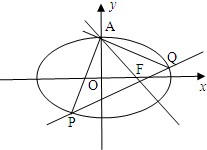 (2012•梅州一模)如图,已知椭圆C:
(2012•梅州一模)如图,已知椭圆C: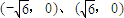 ,O为坐标原点,平行于OM的直线l交椭圆C于不同的两点A、B,
,O为坐标原点,平行于OM的直线l交椭圆C于不同的两点A、B,