题目内容
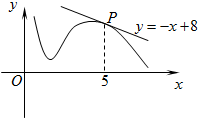
12、如图所示，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f（5）=3
，f′（5）=-1
．分析：根据导数的几何意义知，函数y=f（x）的图象在点P处的切线的斜率就是函数y=f（x）在该点的导数值，因此可求得f′（5），再根据切点的双重性，即切点既在曲线上又在切线上，可求得f（5）．
解答：解：根据图象知，函数y=f（x）的图象与在点P处的切线交于点P，
f（5）=-5+8=3，
f′（5）为函数y=f（x）的图象在点P处的切线的斜率，
∴f′（5）=-1；
故答案为3，-1．
f（5）=-5+8=3，
f′（5）为函数y=f（x）的图象在点P处的切线的斜率，
∴f′（5）=-1；
故答案为3，-1．
点评：此题是个基础题．考查导数的几何意义以及学生识图能力的考查，命题形式新颖．
练习册系列答案
相关题目
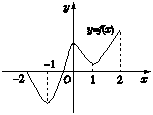
f′（x）是函数y=f（x）的导函数，若y=f′（x）的图象如图所示则函数y=f（x）的图象可能是（ ）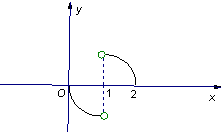
如图所示，函数y=f（x）的图象是圆心在点
)在区间
上的图象，则它的单调增区间是 .