题目内容
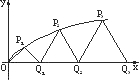 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y=| x |
| 1 |
| 3 |
分析:(1)由题意知P1(
,
).由此可知a1=|OP1|=
.而
×1×2=
,命题成立.
(2)假设n=k(k∈N*)时命题成立,即a1+a2++ak=
k(k+1),则点Qk的坐标为(
k(k+1),0),直线QkPk+1的方程为y=
[x-
k(k+1)].然后用数学归纳法进行证明.
| 1 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
(2)假设n=k(k∈N*)时命题成立,即a1+a2++ak=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
解答:证明:(1)当n=1时,点P1是直线y=
x与曲线y=
的交点,
∴可求出P1(
,
).
∴a1=|OP1|=
.而
×1×2=
,命题成立.
(2)假设n=k(k∈N*)时命题成立,即a1+a2++ak=
k(k+1),
则点Qk的坐标为(
k(k+1),0),
∴直线QkPk+1的方程为y=
[x-
k(k+1)].
代入y=
,解得Pk+1点的坐标为(
,
(k+1))
∴ak+1=|QkPk+1|=
(k+1)•
=
(k+1).
∴a1+a2++ak+ak+1=
k(k+1)+
(k+1)=
(k+1)(k+2).
∴当n=k+1时,命题成立.
由(1)(2)可知,命题对所有正整数都成立.
| 3 |
| x |
∴可求出P1(
| 1 |
| 3 |
| ||
| 3 |
∴a1=|OP1|=
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
(2)假设n=k(k∈N*)时命题成立,即a1+a2++ak=
| 1 |
| 3 |
则点Qk的坐标为(
| 1 |
| 3 |
∴直线QkPk+1的方程为y=
| 3 |
| 1 |
| 3 |
代入y=
| x |
| (k+1)2 |
| 3 |
| ||
| 3 |
∴ak+1=|QkPk+1|=
| ||
| 3 |
| 2 | ||
|
| 2 |
| 3 |
∴a1+a2++ak+ak+1=
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
∴当n=k+1时,命题成立.
由(1)(2)可知,命题对所有正整数都成立.
点评:本题的关键是求出Pk+1的纵坐标,再根据正三角形高与边的关系求出|QkPk+1|.

练习册系列答案
相关题目
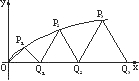 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y= 上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an= n(n+1).
n(n+1).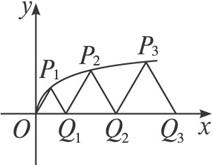
 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y=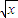 上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an= n(n+1).
n(n+1).