题目内容
直线L过点(1,0)且被两条平行直线L1: 3x+y-6=0和L2: 3x+y+3=0所截得线段长为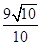 ,则直线L的方程为 (写成直线的一般式)
,则直线L的方程为 (写成直线的一般式)
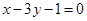
解析试题分析:当直线l的斜率存在时设斜率为k,由直线l过(1,0)得到直线l的方程为y=k(x-1),则联立直线l与3x+y-6=0得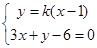 解得
解得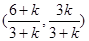 ,同理直线l与3x+y+3=0的交点坐标为
,同理直线l与3x+y+3=0的交点坐标为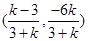 ,则所截得线段长为
,则所截得线段长为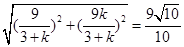 ,解得
,解得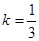 ,故直线为
,故直线为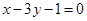 .
.
当直线l的斜率不存在时,直线x=1与两平行直线3x+y-6=0和3x+y+3=0的交点分别为(1,3)与(1,-6),此两点间距离是9,不合.综上直线l的方程为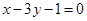 .
.
考点:1.两直线的交点; 2.两点间的距离; 3.直线方程

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 中,若动点
中,若动点 到两直线
到两直线 和
和 的距离之和为
的距离之和为 ,则
,则 的最大值是________.
的最大值是________. 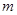 被两条平行直线
被两条平行直线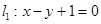 与
与 所截得的线段长为
所截得的线段长为 ,则直线
,则直线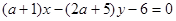 必过一定点,定点的坐标为 .
必过一定点,定点的坐标为 .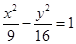 的右焦点为圆心,并与其渐近线相切的圆的标准方程是 _____.
的右焦点为圆心,并与其渐近线相切的圆的标准方程是 _____.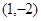 且与直线
且与直线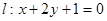 垂直的直线方程为 .
垂直的直线方程为 .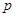 是曲线
是曲线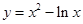 上任意一点,则点
上任意一点,则点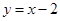 的最小距离为____
的最小距离为____