题目内容
偶函数  在
在
 上单调递增,则
上单调递增,则
 与
与 的大小关系是 ( )
的大小关系是 ( )
A. B.
B.
C. D.
D.
【答案】
D
【解析】本题考查了不等关系与不等式,重点考查了对数函数的单调性,考查了分类讨论的数学思想,属基础题。
因为函数f(x)=loga|x-b|,所以对定义图内任意实数x都有f(-x)=f(x),
即loga|-x-b|=loga|x-b|,所以|-x-b|=|x-b|,所以b=0,
则f(x)=loga|x|,若a>1,则a+1>b+2=2,所以loga|a+1|>loga2,f(a+1)>f(b+2);
若0<a<1,则1<a+1<b+2=2,所以loga|a+1|>loga2,f(a+1)>f(b+2);
综上,f(a+1)>f(b+2).故选D.
解决该试题关键是先由函数为偶函数,求出b的值为0,然后分a>1和0<a<1进行讨论,不论哪种情况,两个变量a+1和b+2均大于1。

练习册系列答案
相关题目
 ,在
,在 上单调递增,则
上单调递增,则 )与
)与 的大小关系是( )
的大小关系是( ) B.
B.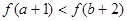
 D.
D. 
 ,则函数
,则函数 的图象与
的图象与 的图象关于直线
的图象关于直线 对称,则函数
对称,则函数 是( )
是( ) 上单调递减 B.偶函数在
上单调递减 B.偶函数在 上单调递减 D.偶函数在
上单调递减 D.偶函数在 在
在 上单调递增,设
上单调递增,设 ,
, ,
, ,则
,则 大小关系是( )
大小关系是( ) B.
B. C.
C.
 D.
D.
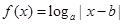 在
在 上单调递增,则
上单调递增,则 的取值范围是 .
的取值范围是 .