题目内容
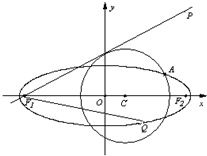 已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E: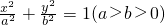 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
(1)求直线PF1的方程;
(2)求椭圆E的方程;
(3)设Q为椭圆E上的一个动点,求证:以QF1为直径的圆与圆x2+y2=18相切.
解:(1)因为A(3,1)在⊙C上,
所以,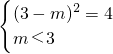 ,m=1.
,m=1.
所以,⊙C:(x-1)2+y2=5.(2分)
易知直线PF1的斜率存在,设直线PF1方程:y-4=k(x-4),
即:kx-y+(4-4k)=0
题设有: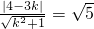 ,
,
 或
或 (4分)
(4分)
 时,直线PF1方程
时,直线PF1方程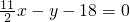 ,
,
令y=0,则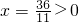 ,不合题意(舍去)
,不合题意(舍去)
 时,直线PF1方程:x-2y+4=0.
时,直线PF1方程:x-2y+4=0.
令y=0,则x=-4<0满足题设.
所以,直线PF1方程为:x-2y+4=0.(6分)
(2)由(1)知F1(-4,0),
所以,F2(4,0),a2-b2=16①(7分)
又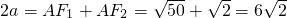
所以,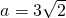 (9分)
(9分)
所以,b2=2(10分)
椭圆E的方程: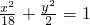 .(11分)
.(11分)
(3)设QF1的中点为M,连QF2.
则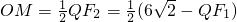 =
= (15分)
(15分)
所以,以QF1为直径的圆内切于圆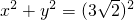 ,
,
即x2+y2=18.(16分)
分析:(1)因为A(3,1)在⊙C上,所以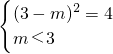 ,m=1.所以⊙C:(x-1)2+y2=5.设直线PF1方程:y-4=k(x-4),由题设知:
,m=1.所以⊙C:(x-1)2+y2=5.设直线PF1方程:y-4=k(x-4),由题设知: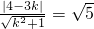 ,
, 或
或 .由此能求出直线PF1方程.
.由此能求出直线PF1方程.
(2)由F1(-4,0),知F2(4,0),a2-b2=16.由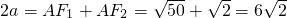 ,知
,知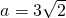 ,b2=2,由此能求出椭圆E的方程.
,b2=2,由此能求出椭圆E的方程.
(3)设QF1的中点为M,连QF2.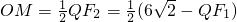 =
= ,由此能证明以QF1为直径的圆与圆x2+y2=18相切.
,由此能证明以QF1为直径的圆与圆x2+y2=18相切.
点评:本题考查直线方程和椭圆方程的求法,证明以QF1为直径的圆与圆x2+y2=18相切.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用圆锥曲线的性质,合理地进行等价转化.
所以,
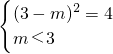 ,m=1.
,m=1.所以,⊙C:(x-1)2+y2=5.(2分)
易知直线PF1的斜率存在,设直线PF1方程:y-4=k(x-4),
即:kx-y+(4-4k)=0
题设有:
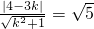 ,
, 或
或 (4分)
(4分) 时,直线PF1方程
时,直线PF1方程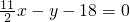 ,
,令y=0,则
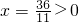 ,不合题意(舍去)
,不合题意(舍去) 时,直线PF1方程:x-2y+4=0.
时,直线PF1方程:x-2y+4=0.令y=0,则x=-4<0满足题设.
所以,直线PF1方程为:x-2y+4=0.(6分)
(2)由(1)知F1(-4,0),
所以,F2(4,0),a2-b2=16①(7分)
又
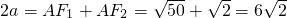
所以,
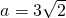 (9分)
(9分)所以,b2=2(10分)
椭圆E的方程:
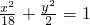 .(11分)
.(11分)(3)设QF1的中点为M,连QF2.
则
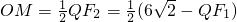 =
= (15分)
(15分)所以,以QF1为直径的圆内切于圆
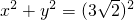 ,
,即x2+y2=18.(16分)
分析:(1)因为A(3,1)在⊙C上,所以
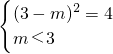 ,m=1.所以⊙C:(x-1)2+y2=5.设直线PF1方程:y-4=k(x-4),由题设知:
,m=1.所以⊙C:(x-1)2+y2=5.设直线PF1方程:y-4=k(x-4),由题设知: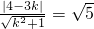 ,
, 或
或 .由此能求出直线PF1方程.
.由此能求出直线PF1方程.(2)由F1(-4,0),知F2(4,0),a2-b2=16.由
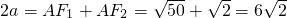 ,知
,知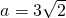 ,b2=2,由此能求出椭圆E的方程.
,b2=2,由此能求出椭圆E的方程.(3)设QF1的中点为M,连QF2.
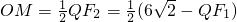 =
= ,由此能证明以QF1为直径的圆与圆x2+y2=18相切.
,由此能证明以QF1为直径的圆与圆x2+y2=18相切.点评:本题考查直线方程和椭圆方程的求法,证明以QF1为直径的圆与圆x2+y2=18相切.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用圆锥曲线的性质,合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
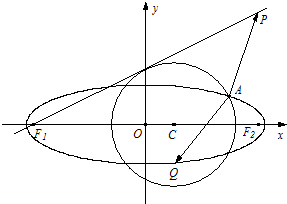 已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E: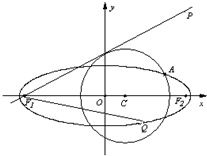 已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E: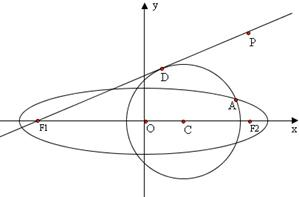 已知点P (4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
已知点P (4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E: 已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E: 与椭圆E:
与椭圆E: 有一个公共点A(3,1),F1.F2分别是椭圆的左.右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1.F2分别是椭圆的左.右焦点,直线PF1与圆C相切.
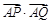 的范围.
的范围.