题目内容
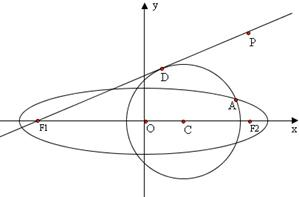 已知点P (4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
已知点P (4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
(1)求m的值与椭圆E的方程.
(2)设D为直线PF1与圆C的切点,在椭圆E上是否存在点Q,使△PDQ是以PD为底的等腰三角形?若存在,请指出共有几个这样的点?并说明理由.
分析:(1)把点A代入圆的方程求得m,设F1(-c,0)则直线PF1的方程可表示出来,根据直线PF1与圆C相切利用点到直线的距离求得c,进而把点(3,1)代入椭圆方程,求得a和b的关系式,同时根据a2-b2=c3,求得a和b的另一个关系式,最后联立求得a和b.则椭圆的方程可得.
(2)把直线方程与圆的方程联立求得切点坐标,进而根据P的坐标求得线段PD的中点进而根据椭圆的右焦点求得直线MF2的斜率进而求得其垂直平线的斜率,进而判断出线段PD的垂直平分线与椭圆有两个交点判断出在椭圆上存在两个点Q,使△PDQ是以PD为底的等腰三角形.
(2)把直线方程与圆的方程联立求得切点坐标,进而根据P的坐标求得线段PD的中点进而根据椭圆的右焦点求得直线MF2的斜率进而求得其垂直平线的斜率,进而判断出线段PD的垂直平分线与椭圆有两个交点判断出在椭圆上存在两个点Q,使△PDQ是以PD为底的等腰三角形.
解答: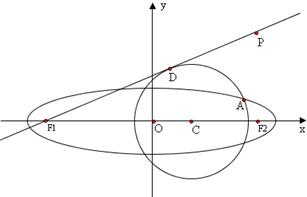 解(1)∵点A(3,1)在圆C上,
解(1)∵点A(3,1)在圆C上,
∴(3-m)2+1=5
又m<3,∴m=1
设F1(-c,0),∵P(4,4)
∴直线PF1的方程
为4x-(4+c)y+4c=0
∵直线PF1与圆C相切
∴
=
(c>0)即c=4
由
解得
∴椭圆E的方程是
+
=1
(2)直线PF1的方程为x-2y+4=0
由
得切点D(0,2)
又∵P(4,4),∴线段PD的中点为M(2,3)
又∵椭圆右焦点F2(4,0)kMF2=
=-
又kPD=
,∴线段PD的垂直平分线的斜率为-2
∵-2<-
,∴线段PD的垂直平分线与椭圆有两个交点
即在椭圆上存在两个点Q,使△PDQ是以PD为底的等腰三角形.
 解(1)∵点A(3,1)在圆C上,
解(1)∵点A(3,1)在圆C上,∴(3-m)2+1=5
又m<3,∴m=1
设F1(-c,0),∵P(4,4)
∴直线PF1的方程
为4x-(4+c)y+4c=0
∵直线PF1与圆C相切
∴
| |4+4c| | ||
|
| 5 |
由
|
|
∴椭圆E的方程是
| x2 |
| 18 |
| y2 |
| 2 |
(2)直线PF1的方程为x-2y+4=0
由
|
又∵P(4,4),∴线段PD的中点为M(2,3)
又∵椭圆右焦点F2(4,0)kMF2=
| 3 |
| 2-4 |
| 3 |
| 2 |
又kPD=
| 1 |
| 2 |
∵-2<-
| 3 |
| 2 |
即在椭圆上存在两个点Q,使△PDQ是以PD为底的等腰三角形.
点评:本题主要考查了直线与圆锥曲线的综合问题.位置关系是历年高考命题的热点;试题具有一定的综合性,覆盖面大,平时应注意多训练.

练习册系列答案
相关题目
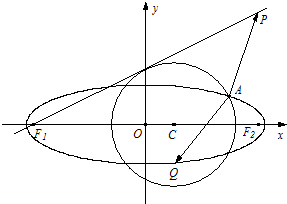 已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E: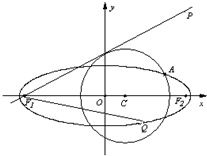 已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E: 已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E: 与椭圆E:
与椭圆E: 有一个公共点A(3,1),F1.F2分别是椭圆的左.右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1.F2分别是椭圆的左.右焦点,直线PF1与圆C相切.
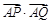 的范围.
的范围.