题目内容
【题目】连续投骰子两次得到的点数分别为m,n,作向量![]() (m,n),则
(m,n),则![]() 与
与![]() (1,﹣1)的夹角成为直角三角形内角的概率是_____.
(1,﹣1)的夹角成为直角三角形内角的概率是_____.
【答案】![]()
【解析】
根据分步计数原理可以得到试验发生包含的所有事件数,满足条件的事件数通过列举得到即可求解
由题意知本题是一个古典概型,
试验发生包含的所有事件数6×6,
∵m>0,n>0,
∴![]() (m,n)与
(m,n)与![]() (1,﹣1)不可能同向.
(1,﹣1)不可能同向.
∴夹角θ≠0.
∵θ∈(0,![]() ]
]
![]()
![]() 0,
0,
∴m﹣n≥0,
即m≥n.
当m=6时,n=6,5,4,3,2,1;
当m=5时,n=5,4,3,2,1;
当m=4时,n=4,3,2,1;
当m=3时,n=3,2,1;
当m=2时,n=2,1;
当m=1时,n=1.
∴满足条件的事件数6+5+4+3+2+1
∴概率P![]() .
.
故答案为:![]()

【题目】据历史记载,美日在中途岛(Midway)海战前,美方截获了日方密码电报,据美方已破译的密码得知,日方将向某岛进行军事活动,但关键含有地点的部分却被日方换成了另一种密码.经专家研究,估计是一种密匙密码,且密匙为3位.所谓密匙密码是指:将一段英文字母的明文(未加密前原文)经过对某一组数字(即密匙)的变换,改变成了另一组英文字母成为密文(加密后的文字)例如:明文:![]() (不计空格,不计大小写)在密匙为:1 9 2的条件下,变换过程如下图所示:
(不计空格,不计大小写)在密匙为:1 9 2的条件下,变换过程如下图所示:
s | t | u | d | e | n | t |
1 | 9 | 2 | 1 | 9 | 2 | 1 |
t | c | w | e | n | p | u |
则密文为:![]() ,试根据上面信息回答下面问题:
,试根据上面信息回答下面问题:
(1)在密匙为111的条件下,填写下表,并写出密文;
s | t | u | d | e | n | t |
密文____________________.
(2)若![]()
![]() 请填写下表,并写出密匙;
请填写下表,并写出密匙;
s | t | u | d | e | n | t |
密匙为_____________.
(3)若下面即是那段包含地点(Midway)的破译不出的密文:![]() ,且此段密文也是3位密匙加密,试填写下表,写出密匙,并将此段密文翻译成明文.(不必证明,写出明文即可)
,且此段密文也是3位密匙加密,试填写下表,写出密匙,并将此段密文翻译成明文.(不必证明,写出明文即可)
c | w | b | c | f | s | o | l | l | y | d | g |
密匙为___________,明文为_________.
【题目】2019年国际篮联篮球世界杯,将于2019年在的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传世界杯,某大学从全校学生中随机抽取了![]() 名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有![]() 的把握认为收看篮球世界杯赛事与性别有关?
的把握认为收看篮球世界杯赛事与性别有关?
(2)现从参与问卷调查且收看篮球世界杯赛事的学生中,采用按性别分层抽样的方法选取![]() 人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
(i)求男、女学生各选取多少人;
(ii)若从这![]() 人中随机选取
人中随机选取![]() 人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到
人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到![]() 名男生的概率.
名男生的概率.
附: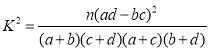 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|