题目内容
曲线C:f(x)=ax3+bx2+cx+d关于原点成中心对称,f(x)极小=f(1)=-
.
(1)求f(x)的解析式;
(2)在曲线C上是否存在点P,使过P点的切线与曲线C除P点以外不再有其它公共点?证明你的结论.
| 2 | 3 |
(1)求f(x)的解析式;
(2)在曲线C上是否存在点P,使过P点的切线与曲线C除P点以外不再有其它公共点?证明你的结论.
分析:1)由函数f(x)图象关于原点对称,知对任意实数x有f(-x)=-f(x),由此能求出f(x)的解析式.
(2)由f'(x)=x2-1,得过P点的切线斜率为k及切线方程,与曲线C的方程联立,考查解的个数,即得到正确的结论.
(2)由f'(x)=x2-1,得过P点的切线斜率为k及切线方程,与曲线C的方程联立,考查解的个数,即得到正确的结论.
解答:解:(1)∵f(x)=ax3+bx2+cx+d的图象关于原点成中心对称,
∴对任意实数x,有f(-x)=-f(x),
即-ax3+bx2-cx+d=-(ax3+bx2+cx+d),
∴2bx2+2d=0对任意x∈R都成立,
∴b=d=0;
又∵f(x)极小=f(1)=-
,
∴f′(x)=3ax2+c,
即3a+c=0,且a+c=-
;
解得a=
,c=-1;
∴f(x)=
x3-x.
(2)∵f(x)=
x3-x,
∴f′(x)=x2-1,
∴过P点的切线斜率为k=f′(x0)=x02-1,
∴切线方程为y-y0=(x02-1)(x-x0)①;
又点P(x0,y0)在曲线C上,∴y0=
x03-x0②;
曲线C:y=
x3-x③;
由①②③化简得:
x3-x02x+
x03=0;
考查函数g(x)=
x3-x02x+
x03,
∵g′(x)=x2-x02,
当x0=0时,g′(x)≥0,g(x)是R上的增函数,有唯一零点x=x0=0,
则过该点P(0,0)的切线y=-x与曲线C除P点以外不再有其它公共点.如图,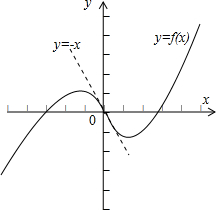
∴对任意实数x,有f(-x)=-f(x),
即-ax3+bx2-cx+d=-(ax3+bx2+cx+d),
∴2bx2+2d=0对任意x∈R都成立,
∴b=d=0;
又∵f(x)极小=f(1)=-
| 2 |
| 3 |
∴f′(x)=3ax2+c,
即3a+c=0,且a+c=-
| 2 |
| 3 |
解得a=
| 1 |
| 3 |
∴f(x)=
| 1 |
| 3 |
(2)∵f(x)=
| 1 |
| 3 |
∴f′(x)=x2-1,
∴过P点的切线斜率为k=f′(x0)=x02-1,
∴切线方程为y-y0=(x02-1)(x-x0)①;
又点P(x0,y0)在曲线C上,∴y0=
| 1 |
| 3 |
曲线C:y=
| 1 |
| 3 |
由①②③化简得:
| 1 |
| 3 |
| 2 |
| 3 |
考查函数g(x)=
| 1 |
| 3 |
| 2 |
| 3 |
∵g′(x)=x2-x02,
当x0=0时,g′(x)≥0,g(x)是R上的增函数,有唯一零点x=x0=0,
则过该点P(0,0)的切线y=-x与曲线C除P点以外不再有其它公共点.如图,

点评:本题考查了利用导数求闭区间上函数最值的应用问题以及利用导数求曲线上的斜率与切线方程问题,是综合性强,难度大的题目.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目