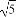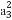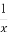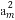Question

在数列{an}中,若对任意的n均有an+an+1+an+2为定值(n∈N*),且a7=2,a9=3,a98=4,则此数列{an}的前100项的和S100=　　　　.

 

Answer 1

299

【解析】设定值为M,则an+an+1+an+2=M,进而an+1+an+2+an+3=M,后式减去前式得an+3=an,即数列{an}是以3为周期的数列.由a7=2,可知a1=a4=a7=…=a100=2,共34项,其和为68;由a9=3,可得a3=a6=…=a99=3,共33项,其和为99;由a98=4,可得a2=a5=…=a98=4,共33项,其和为132.故数列{an}的前100项的和S100=68+99+132=299.