题目内容
在数列1,1,2,3,5,8,x,21,34,55中,x等于( )
A.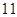 | B.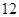 | C.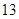 | D.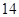 |
C
解析试题分析:从已知数列观察出特点:从第三项开始每一项是前两项的和即可求解
∵数列1,1,2,3,5,8,x,21,34,55 设数列为{an}∴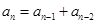 (n>3)
(n>3)
∴x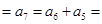 5+8=13
5+8=13
故选C
考点:数列的概念
点评:本题考查了数列的概念及简单表示法,是斐波那契数列,属于基础题.

练习册系列答案
相关题目
已知数列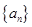 的前n项和
的前n项和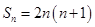 ,则
,则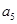 的值为( )
的值为( )
| A.80 | B.40 | C.20 | D.10 |
观察这列数:1,2,3,2,1,2,3,4,3,2,3,4,5,4,3,4,5,6,5,4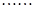 ,则第2013个数是( )
,则第2013个数是( )
| A. 403 | B. 404 | C.405 | D. 406 |
数列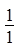 、
、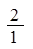 、
、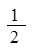 、
、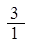 、
、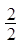 、
、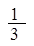 、
、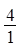 、
、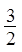 、
、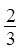 、
、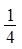 ……依次排列到第
……依次排列到第 项属于的范围是( )。
项属于的范围是( )。
A.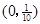 | B.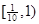 | C.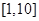 | D.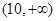 |
数列{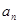 }中,
}中,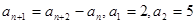 ,则
,则 为( )
为( )
| A.-3 | B.-11 | C.-5 | D.19 |
在数列1,1,2,3,5,8,x,21,34,55,…中,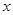 等于( )
等于( )
| A.11 | B.12 | C.13 | D.14 |
已知数列1,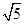 ,3,
,3,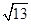 ,…,则
,…,则 可以是这个数列的 ( )
可以是这个数列的 ( )
| A.第5项 | B.第6项 | C.第7项 | D.第8项 |
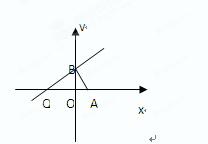
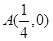 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若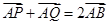 ,
,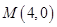 .
.
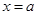 ,以PM为直径的圆与直线
,以PM为直径的圆与直线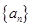 中,
中,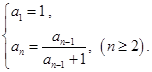 则
则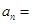 .
.